Die App illustriert die Tatsache, dass die Flächenfunktion A(x) (Fläche zwischen der Funktion f, der x-Achse, einer linken vertikalen Begrenzung a und einer rechten vertikalen Begrenzung x) eine Stammfunktion der Funktion f ist. In anderen Worten: die Ableitung der Flächenfunktion ist f. Um dies nachzuvollziehen, wähle zunächst x (weißer Kringel). Dann lasse h mit Hilfe des Schiebereglers langsam gegen 0 wandern. Das blau schraffierte Flächenstück hat dabei den Flächeninhalt A(x+h)-A(x). Dies ist „beinahe“ die Ableitung von A(x): Man muss diesen Ausdruck nur noch durch h dividieren und dann h gegen 0 gehen lassen (Differentialquotient). Wie können wir einsehen, dass diese Ableitung genau f(x) ist? Trick: Das blau schraffierte Flächenstück wird von dem weißen Rechteck (Fläche: h*f(x)) und dem orangefarbenen Rechteck (Fläche: h*f(x+h)) „eingequetscht“ (siehe linker Formelblock: der blaue Wert liegt zwischen dem weißen und dem orangefarbenen Wert). Jetzt teilt man jeden dieser drei Ausdrücke durch h und erhält dann, dass der Differenzenquotient von A(x) (also „fast“ schon die Ableitung!) zwischen f(x) und f(x+h) „eingequetscht“ ist. Jetzt lässt man h gegen 0 wandern, um die Dinge „festzuzurren“. Im Limes sind alle drei Werte gleich groß, und die Behauptung ist bewiesen.
Frage: f muss stetig sein, damit der Trick funktioniert. Warum?


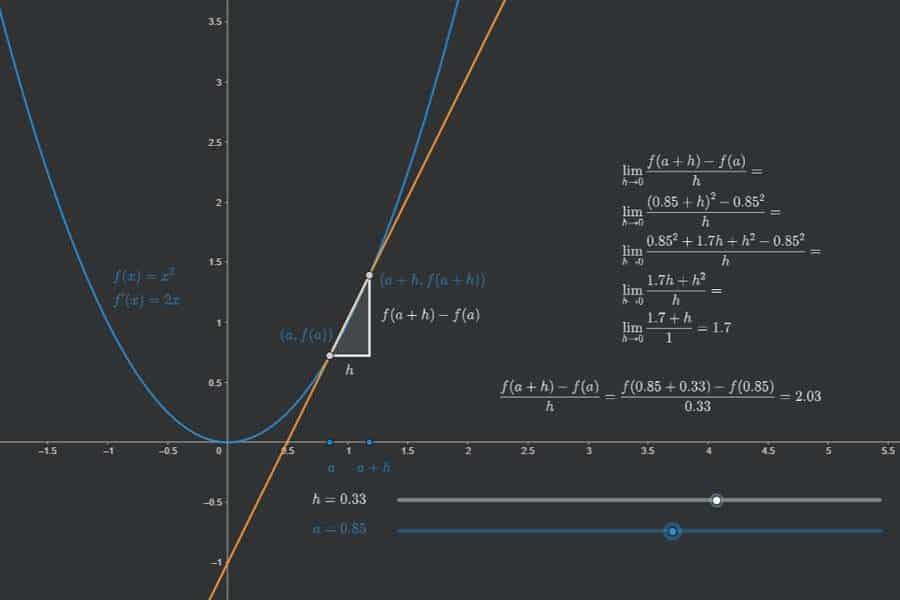
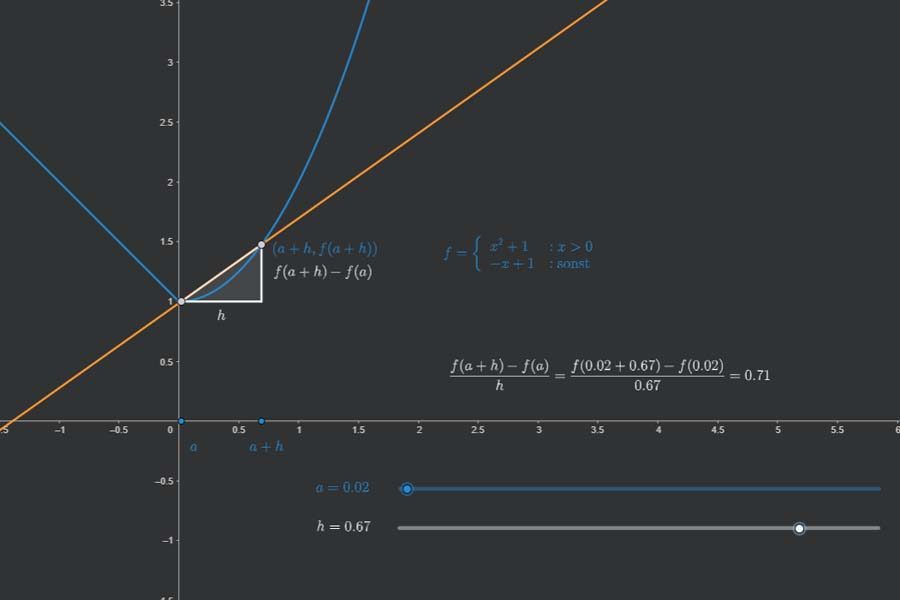
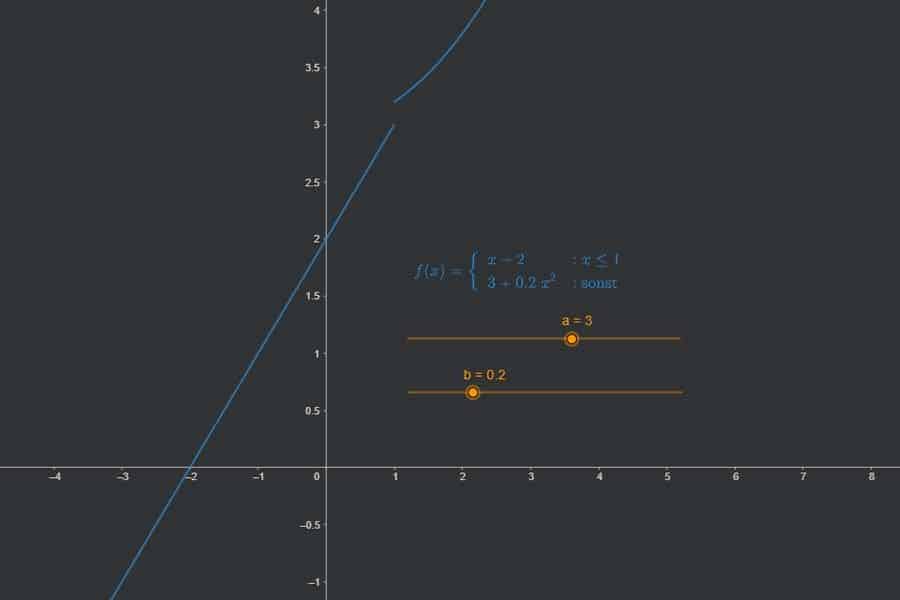
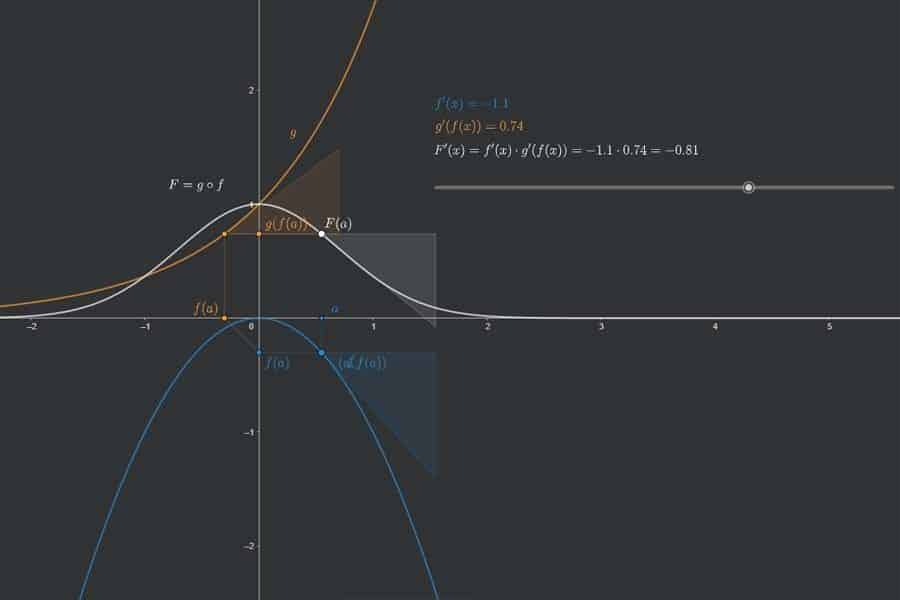
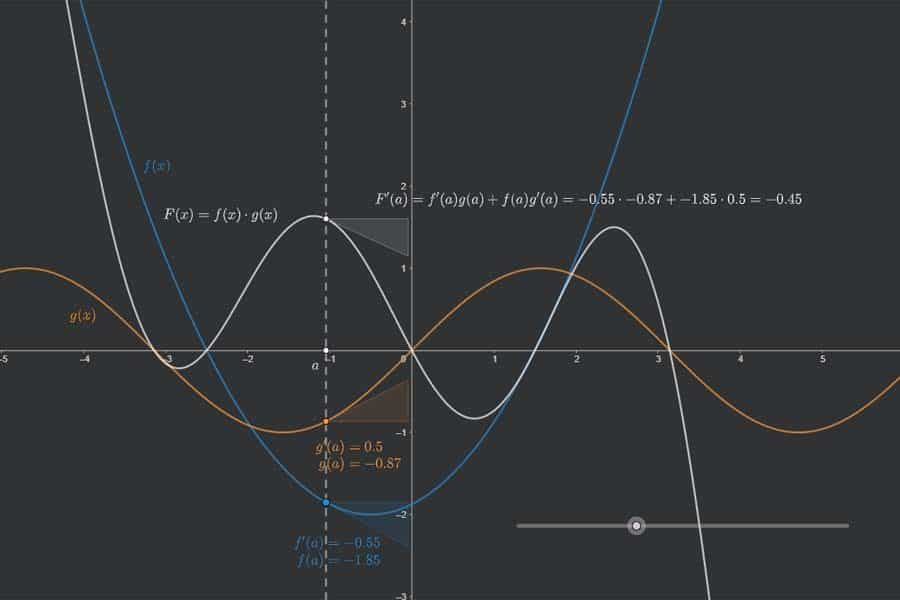
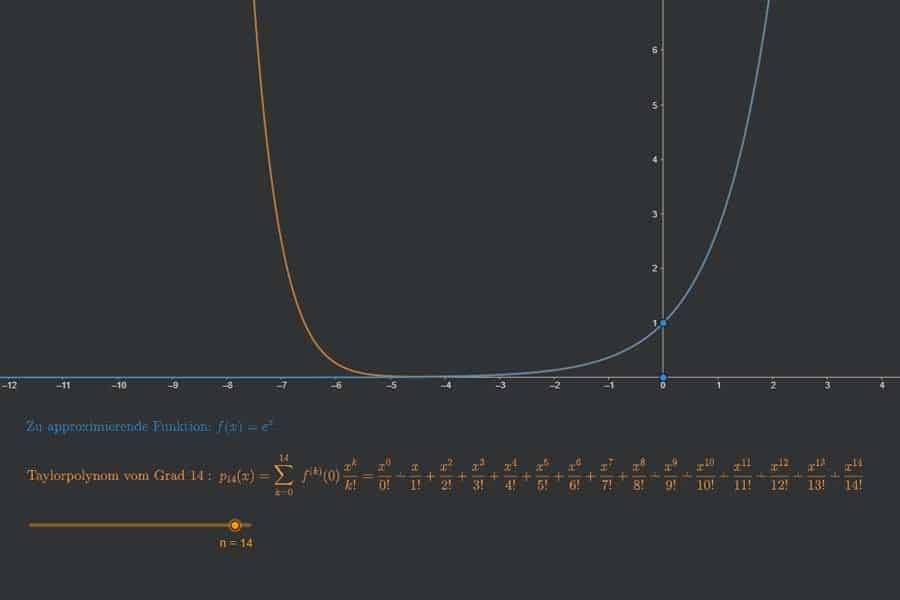
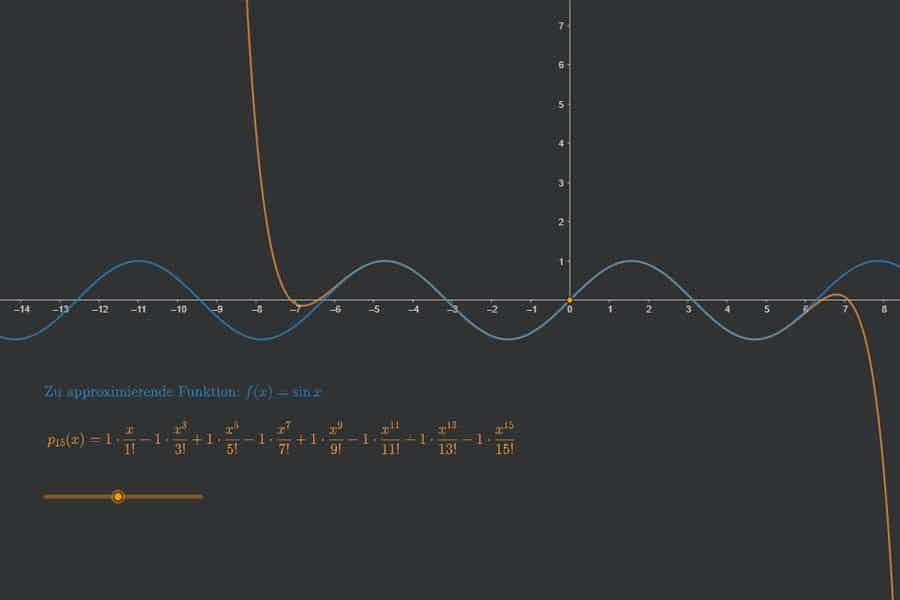
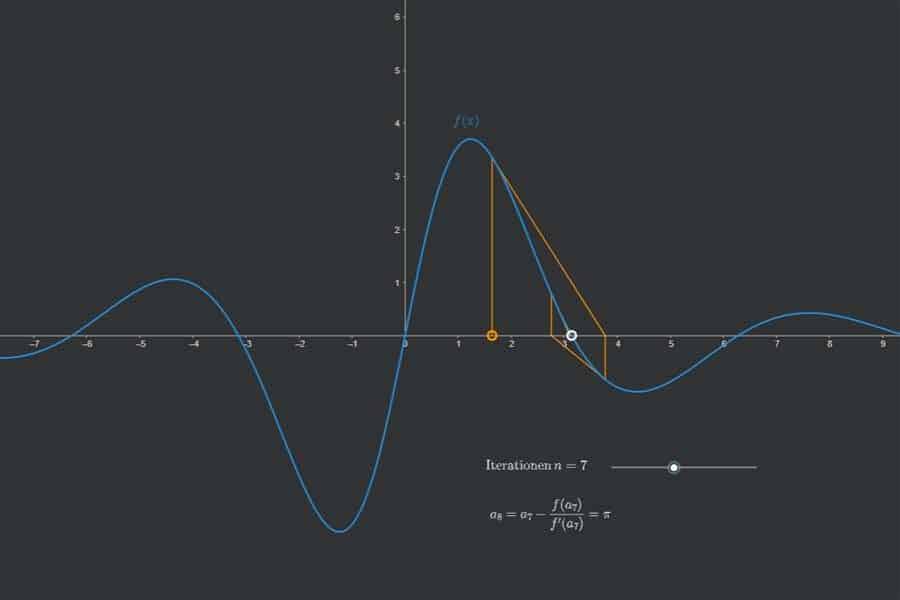











Interaktiv: Ableitung der Umkehrfunktion