Manche Differentialgleichungen lassen sich besonders griffig mit Steigungsfeldern illustrieren.
„Schwierige“ Funktionen mit „simplen“ Funktionen (= Polynomen) approximieren? Herr Taylor hat die Lösung – die nach ihm benannte Reihe. Macht die härtesten Funktionen weich wie Butter. Wir rücken hier speziell der Sinusfunktion zu Leibe. Brauchen tun wir das alltäglich – allein schon unsere heißgeliebten Taschenrechner (Stichwort: „Moment, ich muss mal eben 1+1 tippen…“) sähen blass aus, wenn es die Taylor-Reihe nicht gäbe.


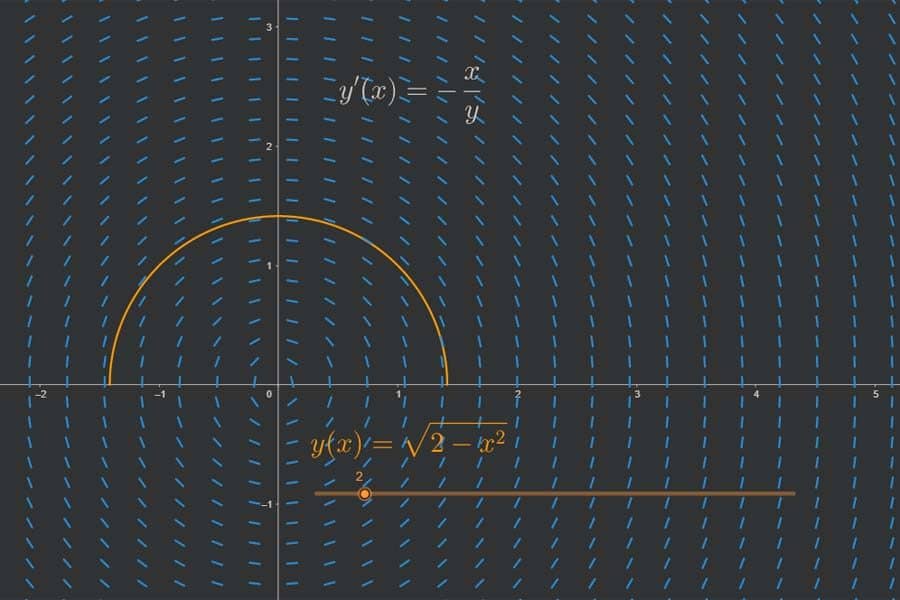
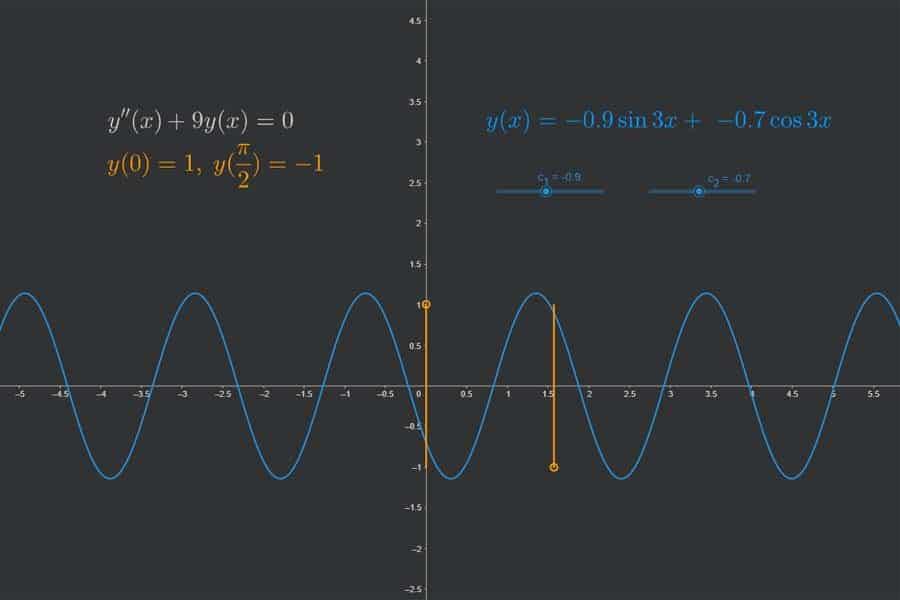

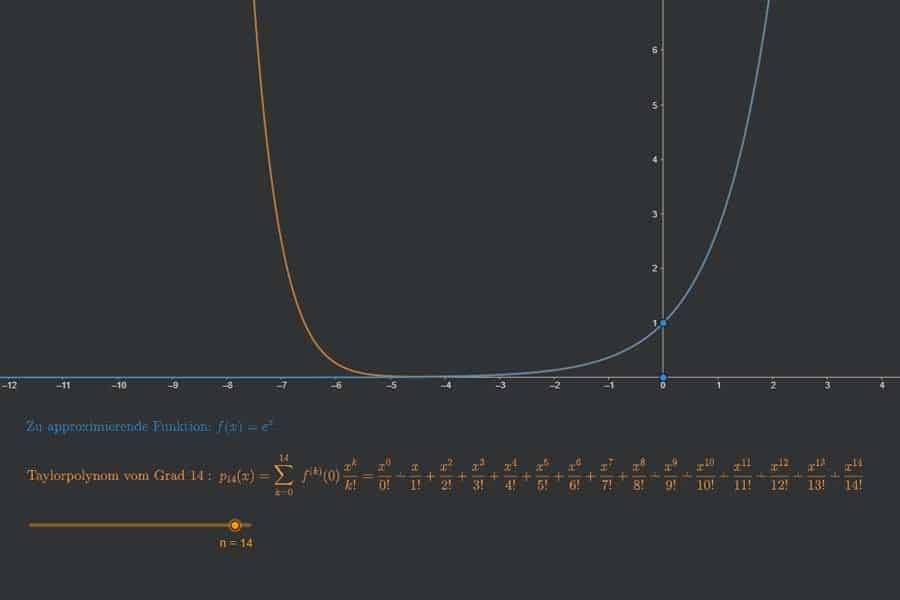
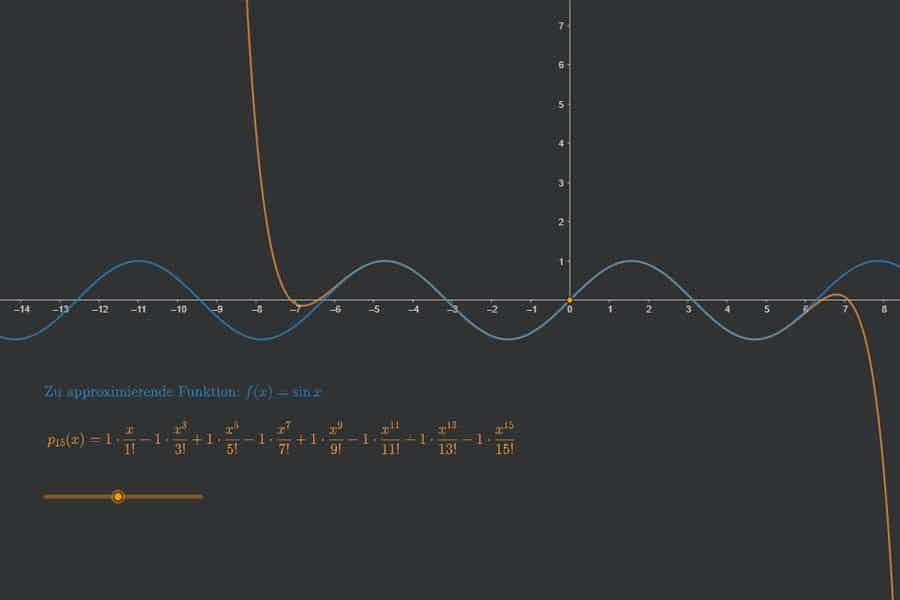











Interaktiv: Richtungsfeld und Trajektorien einer Differentialgleichung