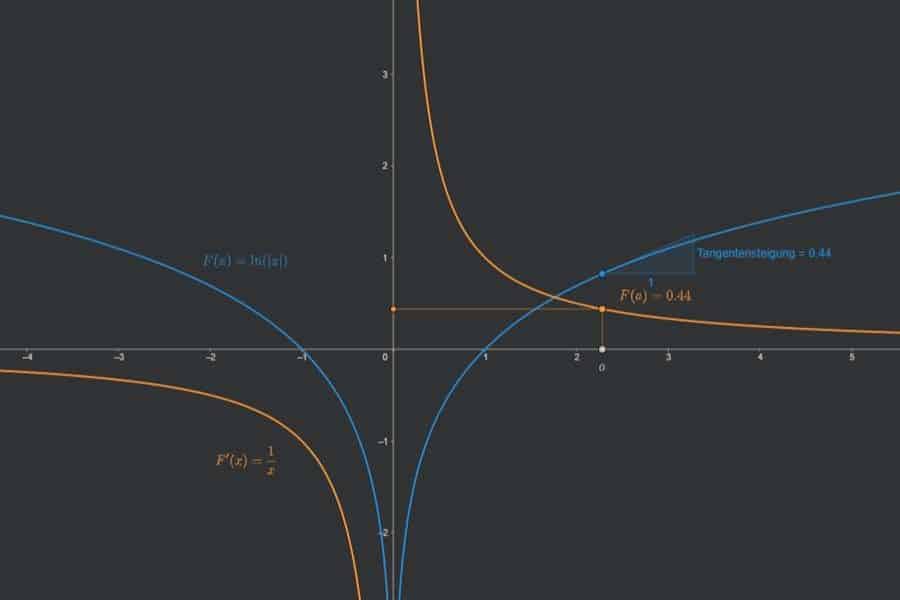
Funktion in Spiegelschrift. Ableitung in Spiegelschrift. Mit Bild ist die Lösung so einfach.
Integrale, d. h. Flächen unter Kurven, müssen mathematisch sauber definiert werden (gerade auch dann, wenn keine Stammfunktion vorliegt oder bekannt ist). Das geht so, dass man „unsauber“ beginnt, indem man die Fläche mit Rechtecken fester Breite auslegt und dabei Fehler in Kauf nimmt. Diese feste Rechteckbreite lässt man dann gegen null gehen, wodurch eine Folge von Säulenauslegungen entsteht, bei denen die Genauigkeit immer weiter zunimmt. Dadurch hat man eine Folge von fehlerhaften Flächeninhaltsmessungen. Jetzt packt man den Begriff des Folgengrenzwerts aus: wenn die Folge einen Grenzwert hat (muss nicht immer der Fall sein), dann ist dieser Grenzwert das Integral. So zumindest der Ansatz von Bernhard Riemann.


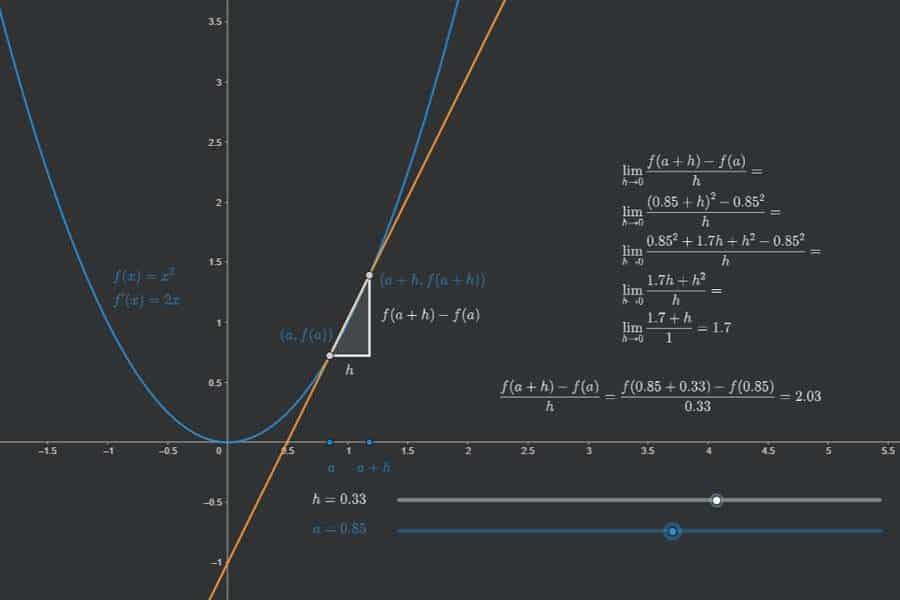
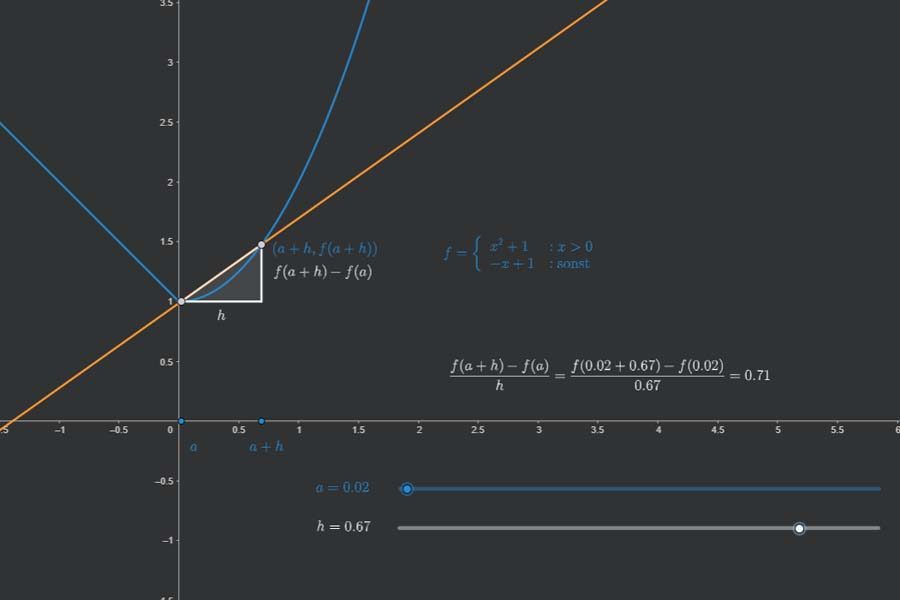
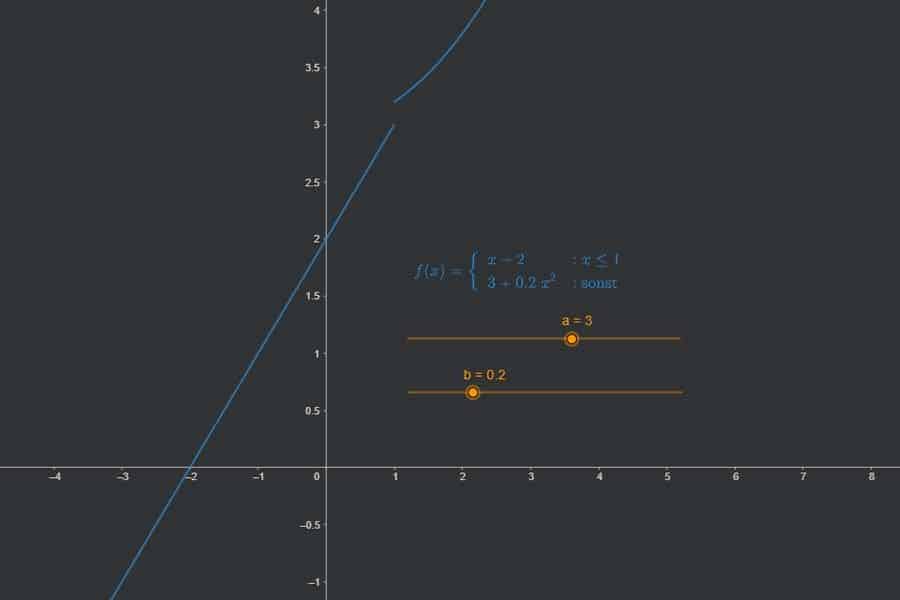
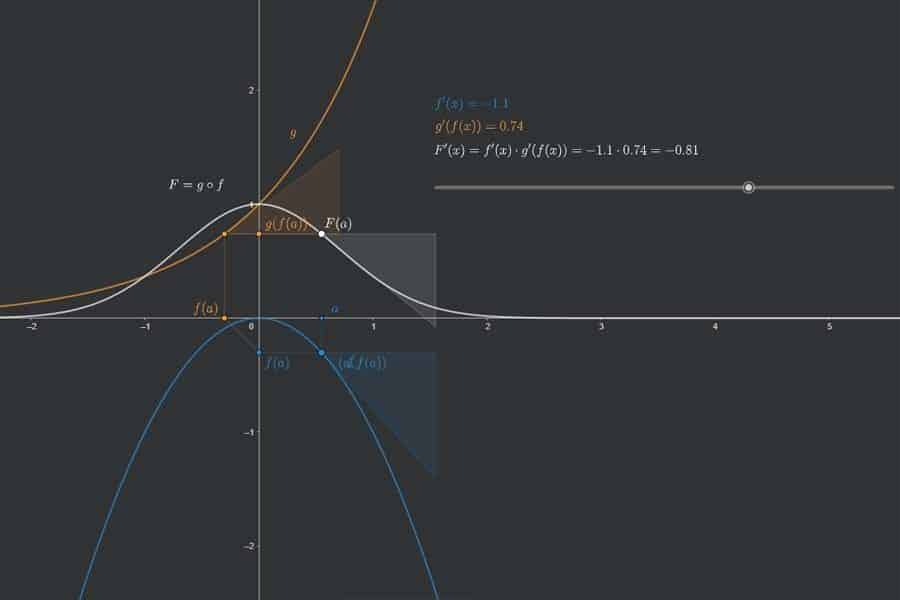
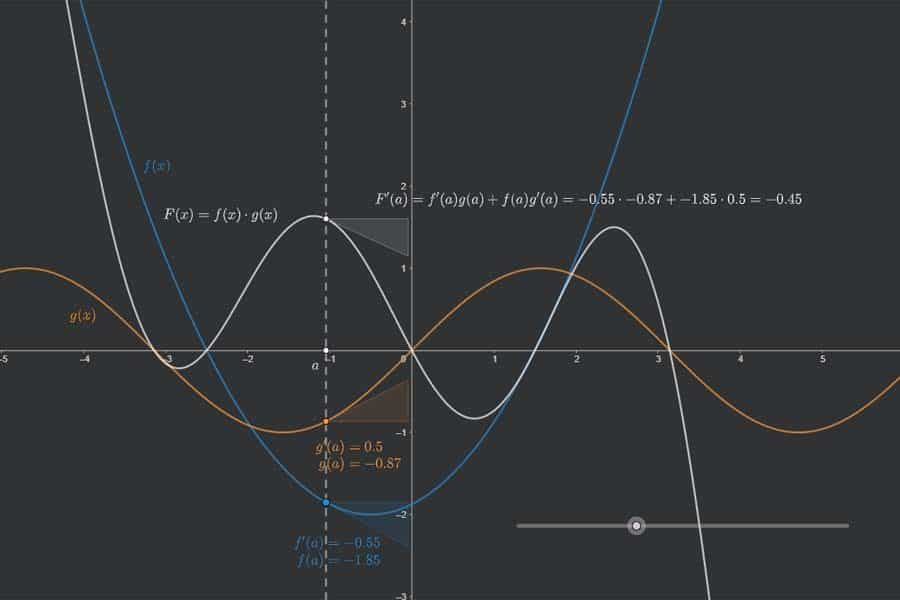
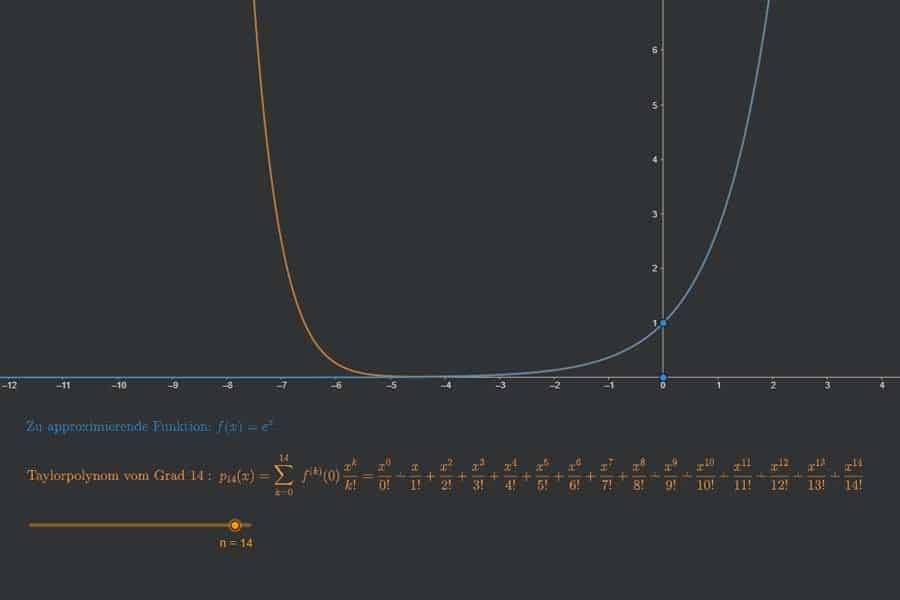
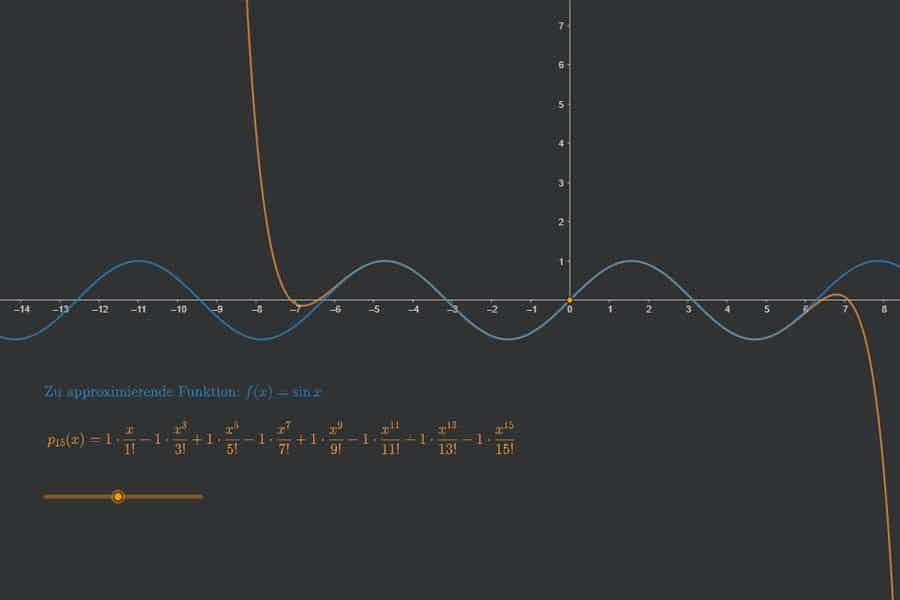
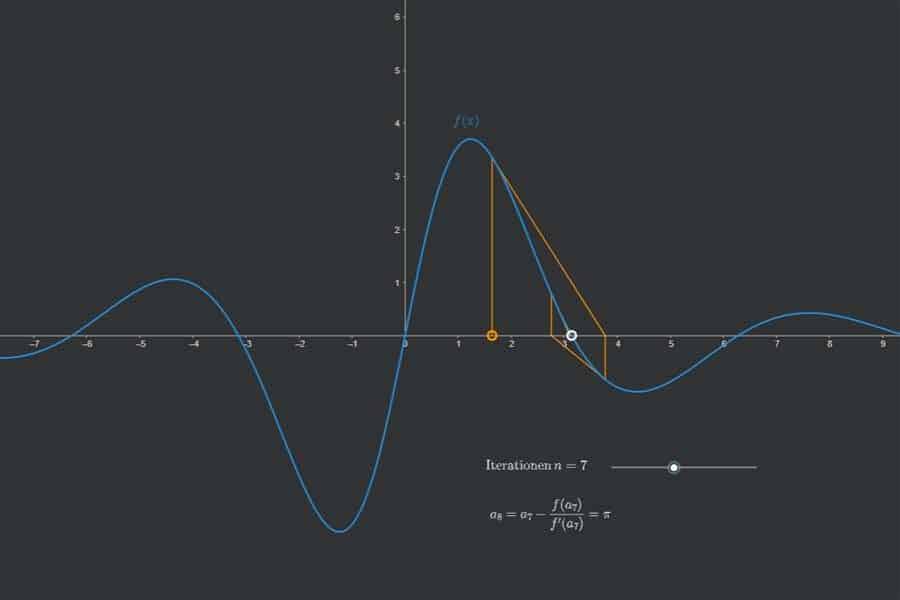











Interaktiv: Ableitung der Umkehrfunktion