Funktion in Spiegelschrift. Ableitung in Spiegelschrift. Mit Bild ist die Lösung so einfach.
Original- und Umkehrfunktionen sind wie Gift und Gegengift. Wenn man sie beide anwendet, ist alles wie vorher. Wie aber verhalten sich ihre Ableitungen zueinander? Die Antwort ist einfach, wenn man weiß, dass die Schaubilder von Gift und Gegengift, äh, Original und Umkehrfunktion Spiegelbilder voneinander sind. An der ersten Winkelhalbierenden. Dann nämlich sind auch die Tangenten und deren Steigungsdreiecke Spiegelbilder, bei denen horizontal und vertikal vertauscht wird. Das ist der Schlüssel zur Lösung: Zähler und Nenner der Steigungen (Ableitungen!) sind vertauscht – klug gesprochen: Kehrwert. Bäm.


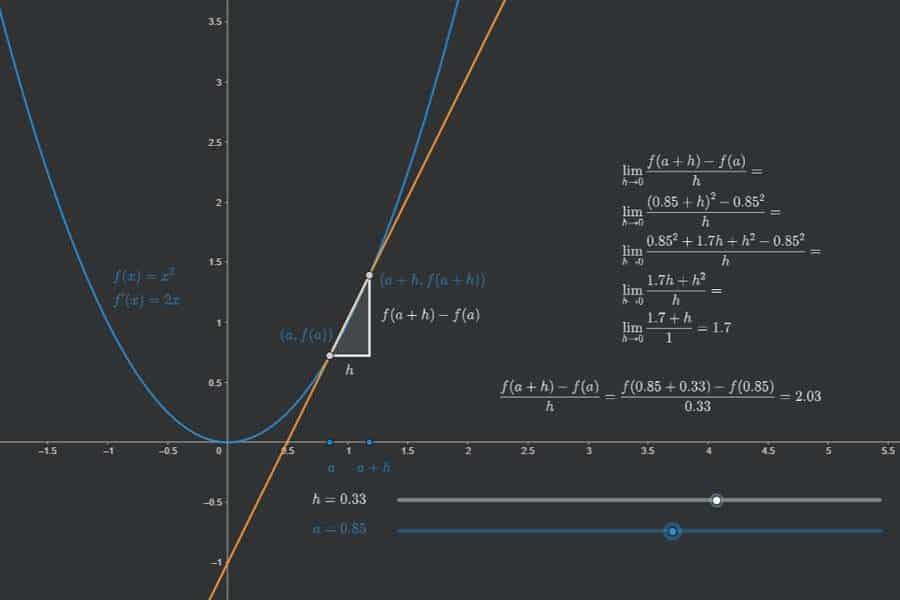
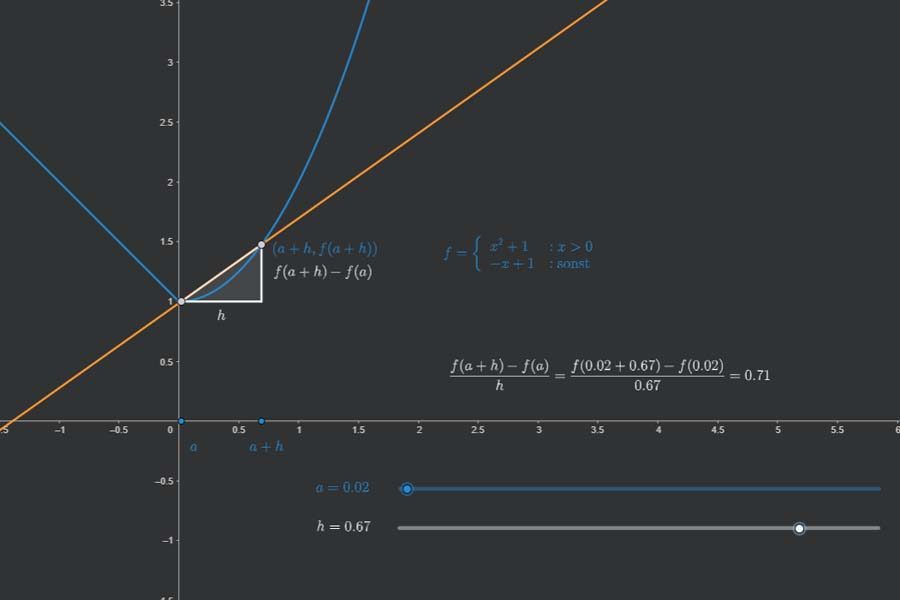
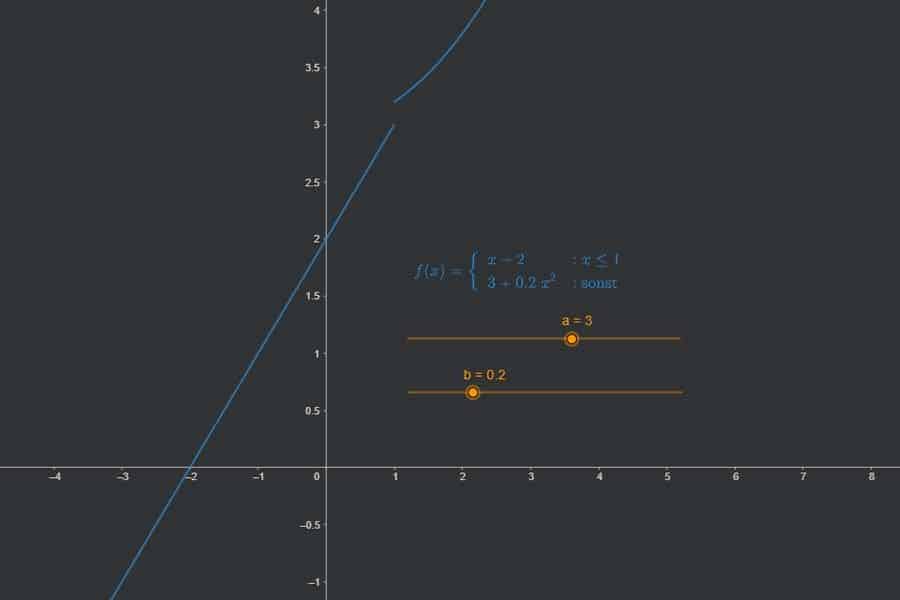
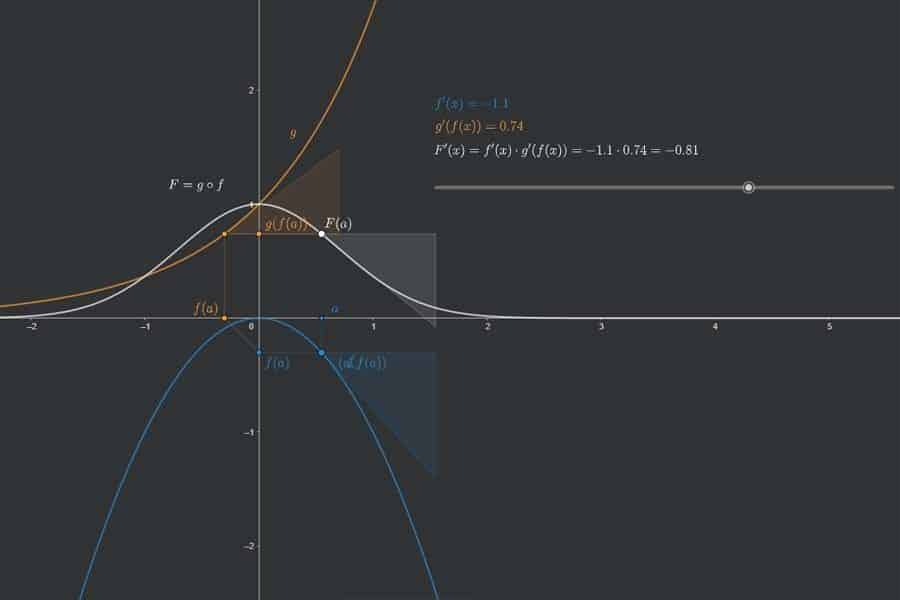
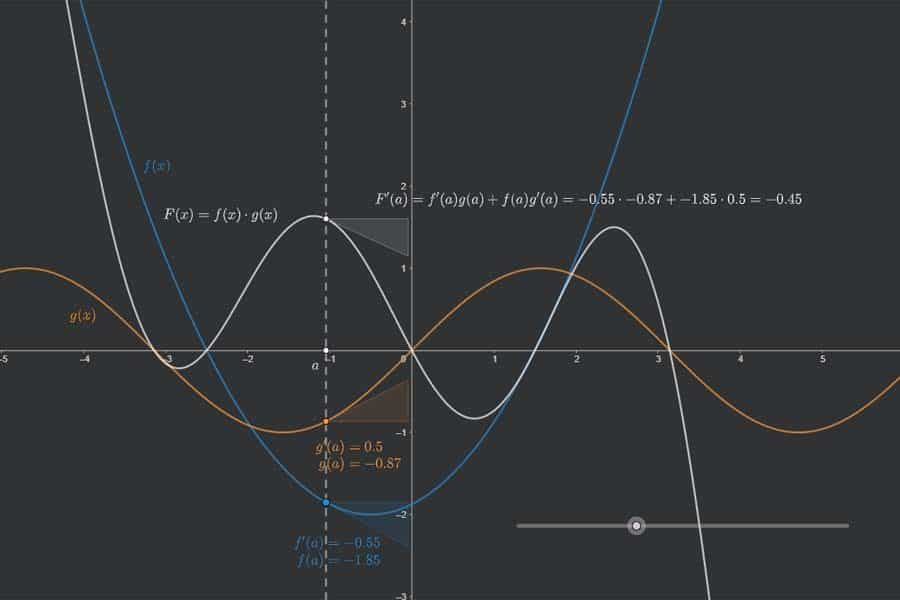
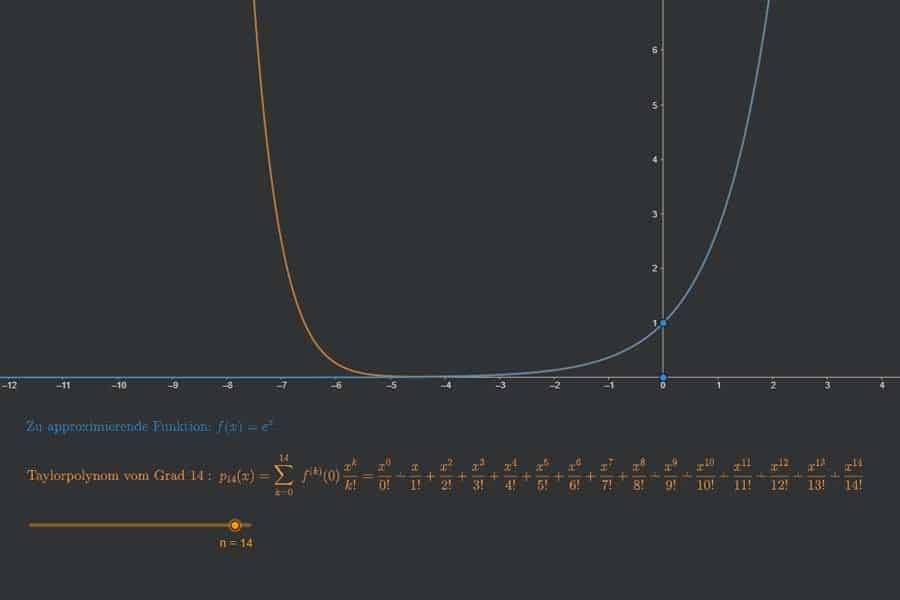
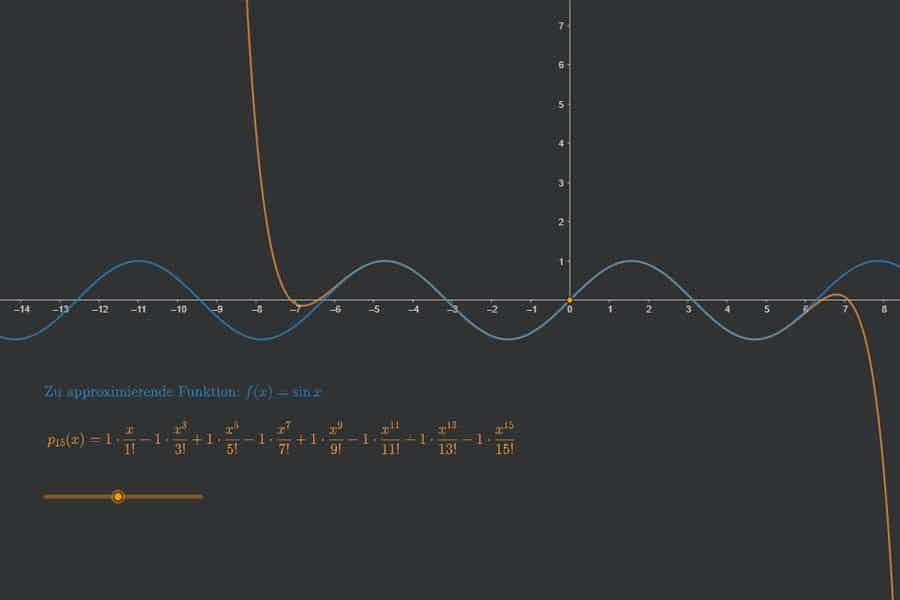
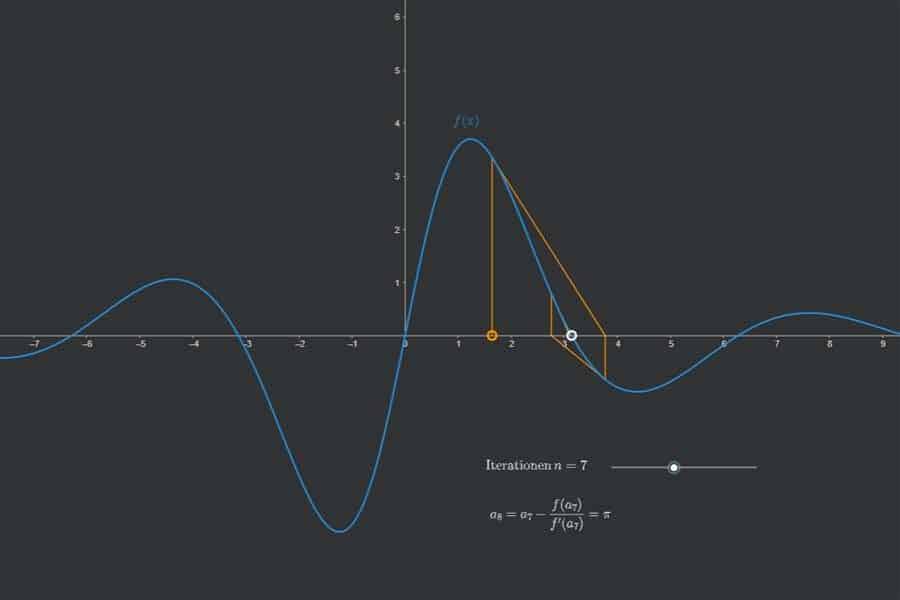
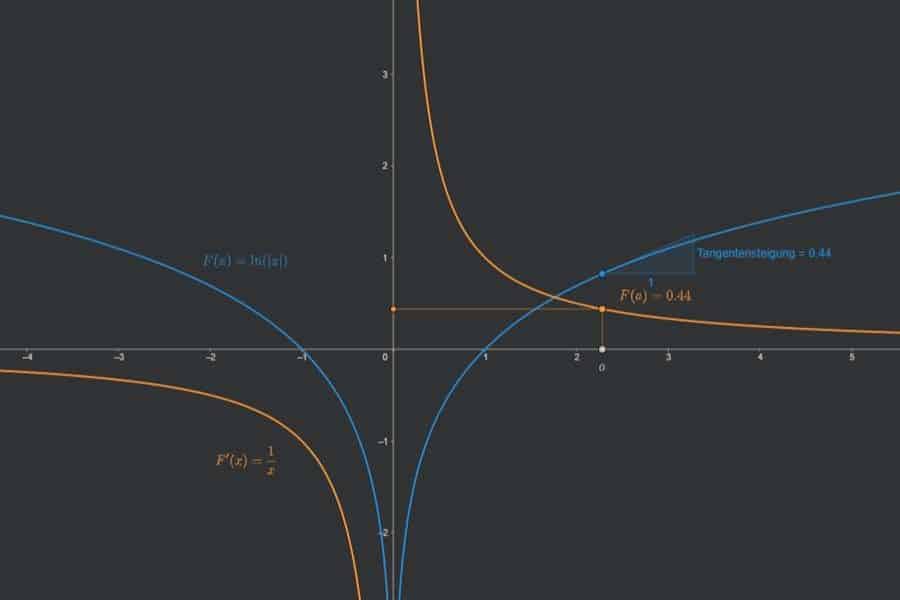











Interaktiv: Ableitung der Umkehrfunktion