Wie hätten Sie Ihre komplexe Zahl gern? Kartesisch, polar oder nach Euler-Art? Wir haben alles.
Angenommen: Wir wollen eine komplexe Zahl mit einer anderen addieren. Dann geht das nur in kartesischer Darstellung, d. h. beide Zahlen müssen in kartesischer Darstellung vorliegen. Wenn das nicht so ist, müssen wir sie in diese Darstellung umwandeln. Führt kein Weg dran vorbei.


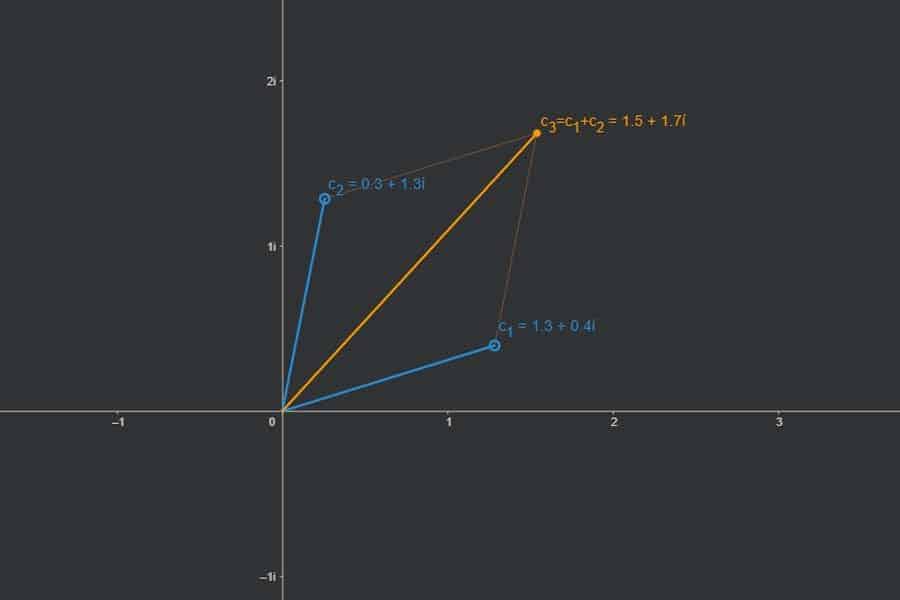
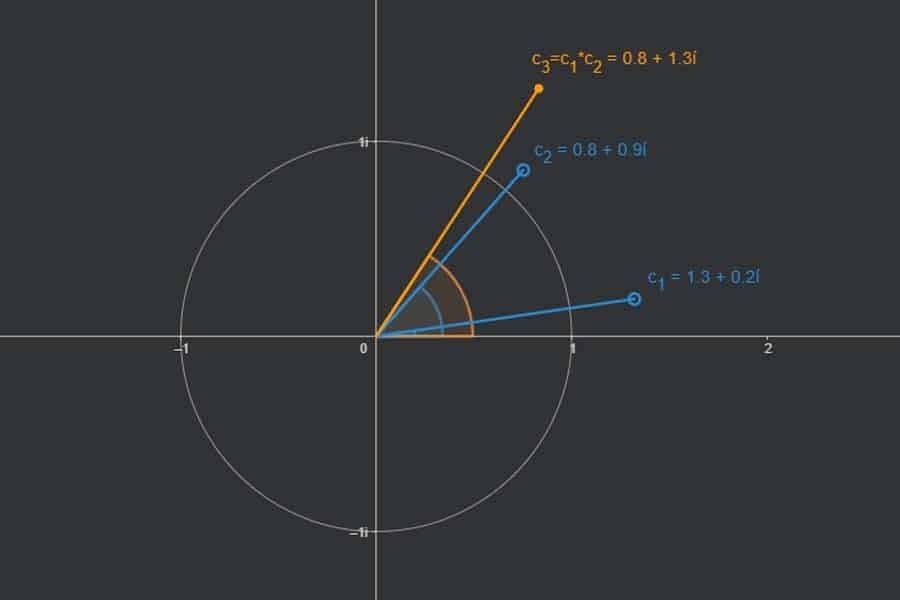
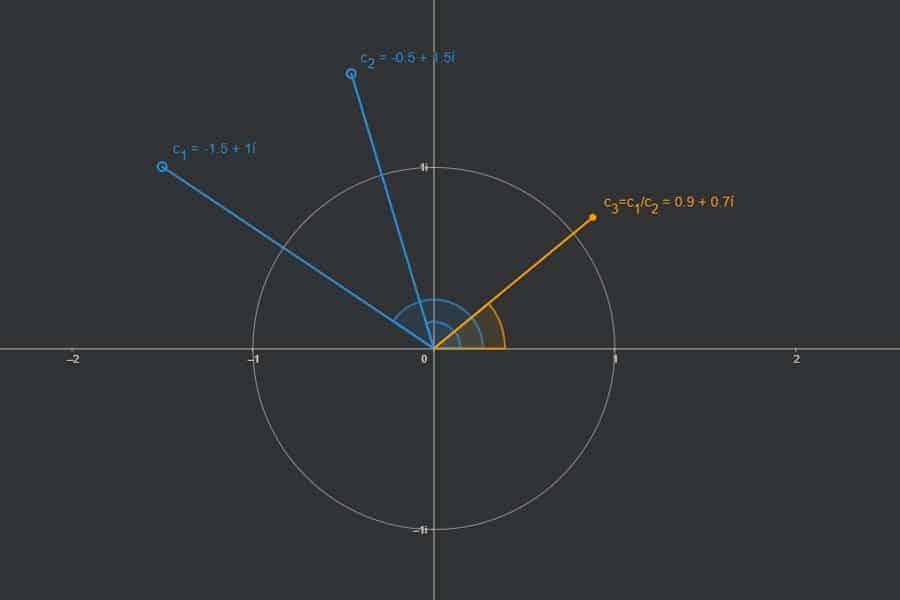













Interaktiv: Darstellungen komplexer Zahlen