Weihnachtsferien: Jeden Tag ein halbes Kilo zunehmen. Diese Folge kennt das Problem.
Die arithmetische Folge beschreibt Prozesse, in denen eine Größe Schritt für Schritt um immer denselben Betrag zunimmt (oder abnimmt). Zum Beispiel wenn ich über die Weihnachtsfeiertage jeden Tag ein halbes Kilo zunehme. Die arithmetische Reihe ist ebenfalls eine (Zahlen-)Folge, die sich ergibt, wenn man für jede natürliche Zahl n die ersten n Glieder einer arithmetischen Folge addiert – also alle meine Gewichte vom ersten Tag der Weihnachtsferien bis zum n-ten Tag aufaddiert (warum auch immer man so etwas tun wollte).


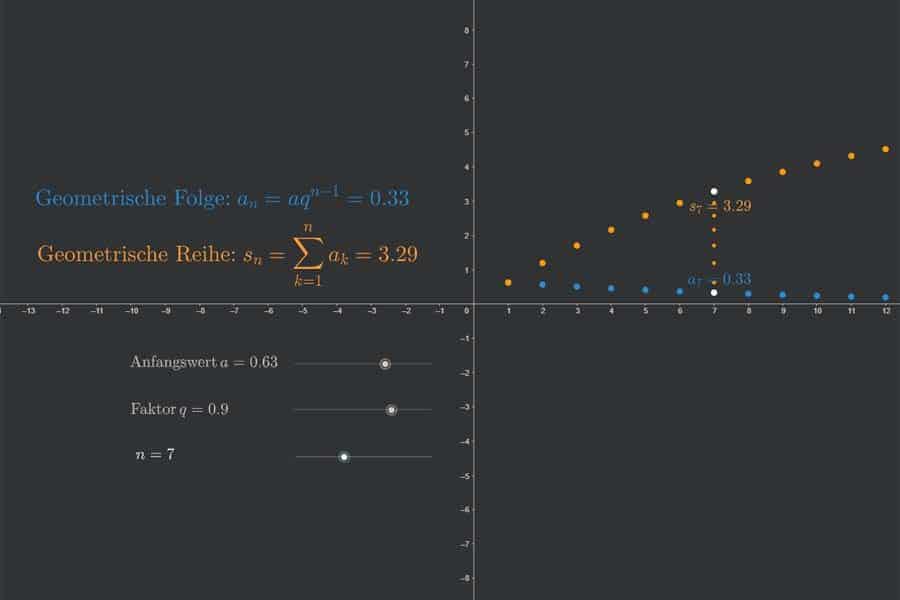
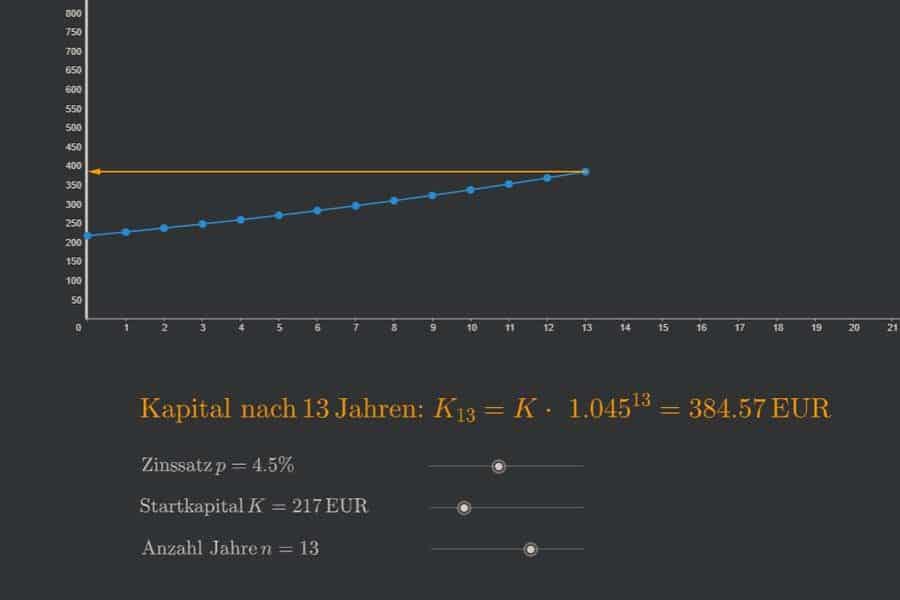
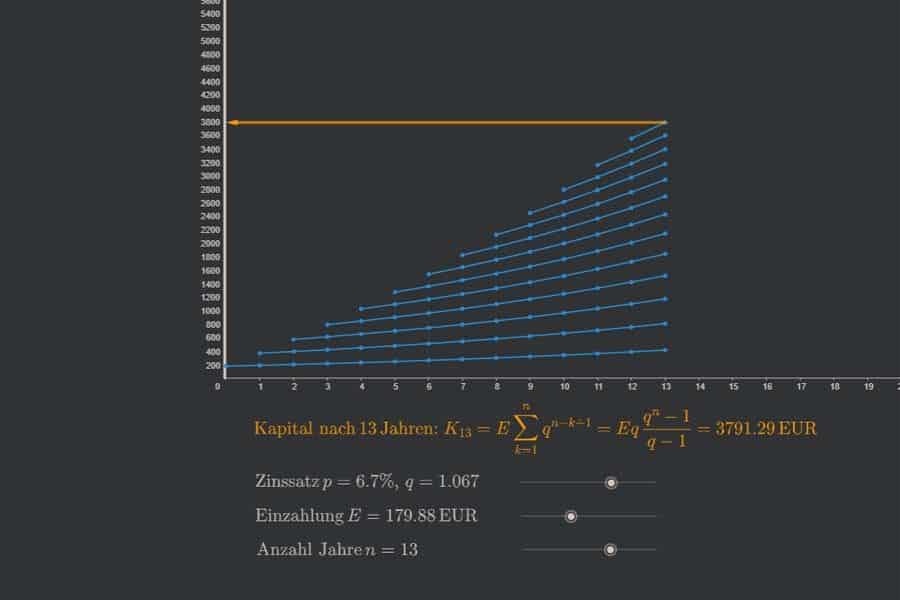
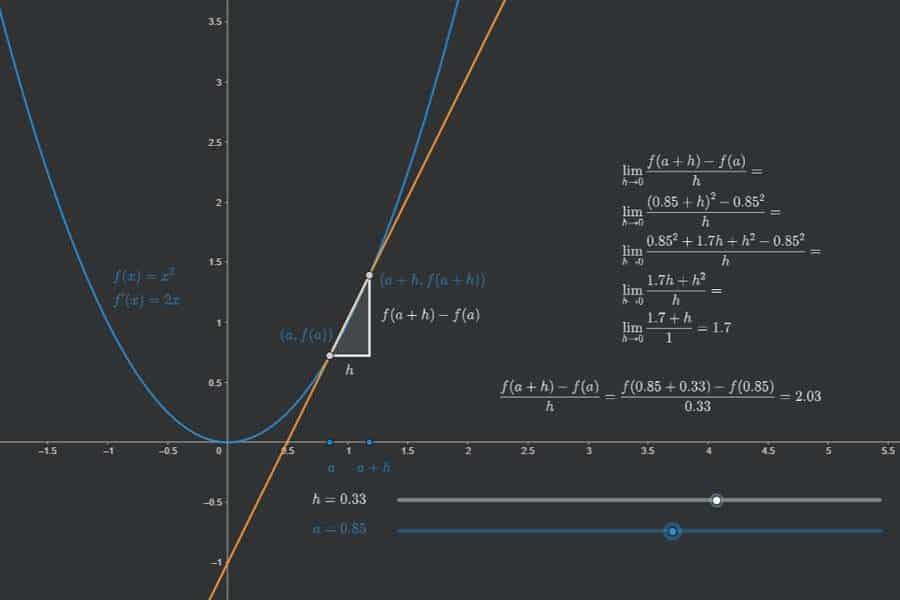











Interaktiv: Arithmetische Folge und Reihe