Bewege den blauen Schieberegler, um Formel und Form der Funktion f einzustellen. Je nach Einstellung hat f am Punkt (0,0) entweder ein lokales Minimum (wenn c kleiner als 2 ist) oder einen Sattelpunkt (wenn c größer als 2 ist). Als Kriterium für ein lokales Minimum könnte man fälschlicherweise annehmen, dass es im Falle einer horizontalen Tangentialfläche („beide ersten partiellen Ableitungen sind 0“) ausreicht, dass die beiden zweiten partiellen Ableitungen fxx und fyy positiv, d. h. dass die beiden gelben Kurven am Punkt (0,0) konvex (nach oben gekrümmt) sind. Dass dies nicht stimmt, sieht man, wenn man c>2 einstellt (f hat dann einen Sattelpunkt am Punkt (0,0)) und am orangefarbenen Schieberegler („Rotation“) die Funktion f um die z-Achse rotieren lässt. Dabei durchläuft man Situationen, in denen beide gelben Kurven nach oben gekrümmt sind, obwohl ein Sattelpunkt (und damit kein lokales Minimum) vorliegt. Das zeigt, dass das oben genannte Kriterium für ein lokales Minimum tatsächlich falsch bzw. noch nicht ausreichend streng ist. Tatsächlich muss nämlich zusätzlich, wie in den Videos erklärt, der Ausdruck Δ am Punkt (0,0) größer 0 sein (siehe weiße Formeln).


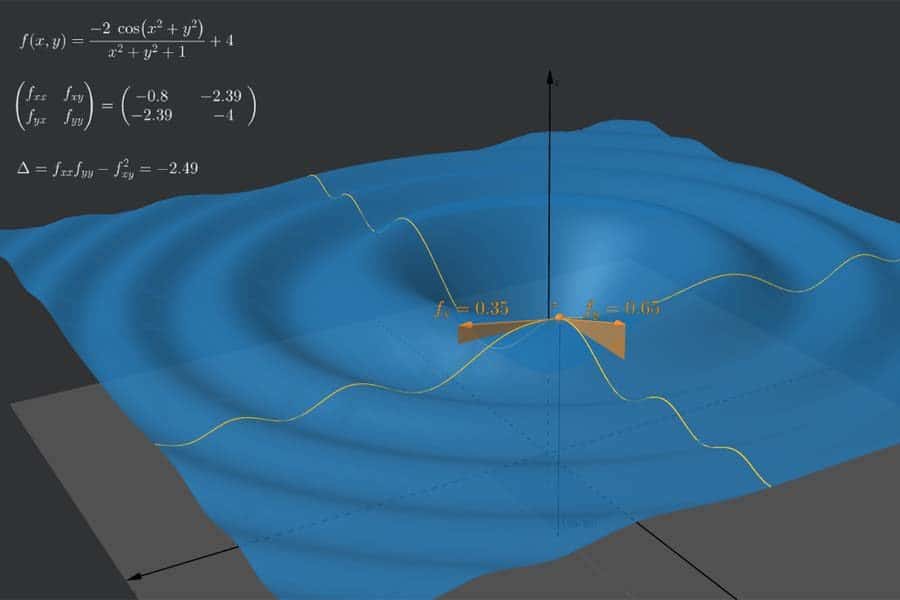












Interaktiv: Zweidimensionale Fläche und partielle Ableitungen