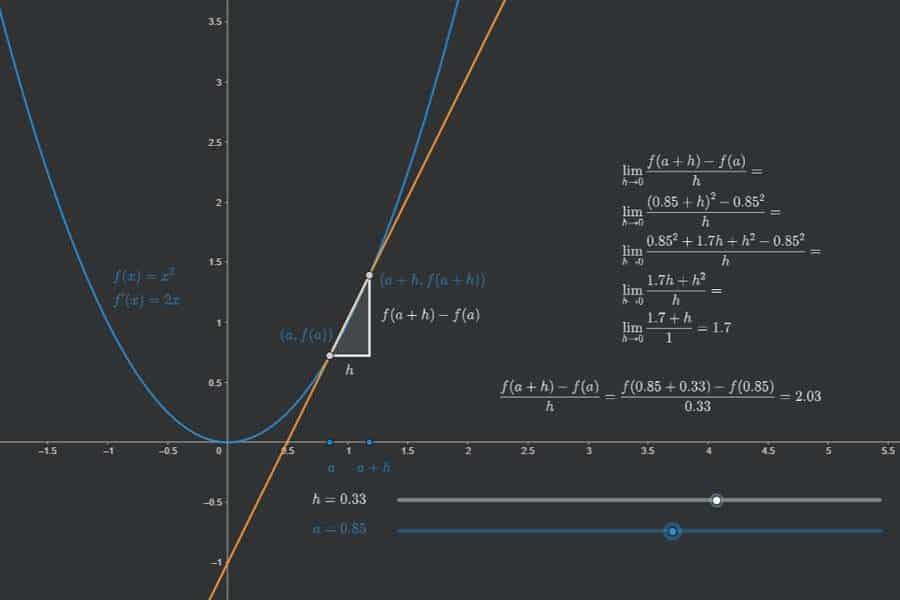
Interaktiv: Berechnung der Ableitung mit dem Differentialquotienten

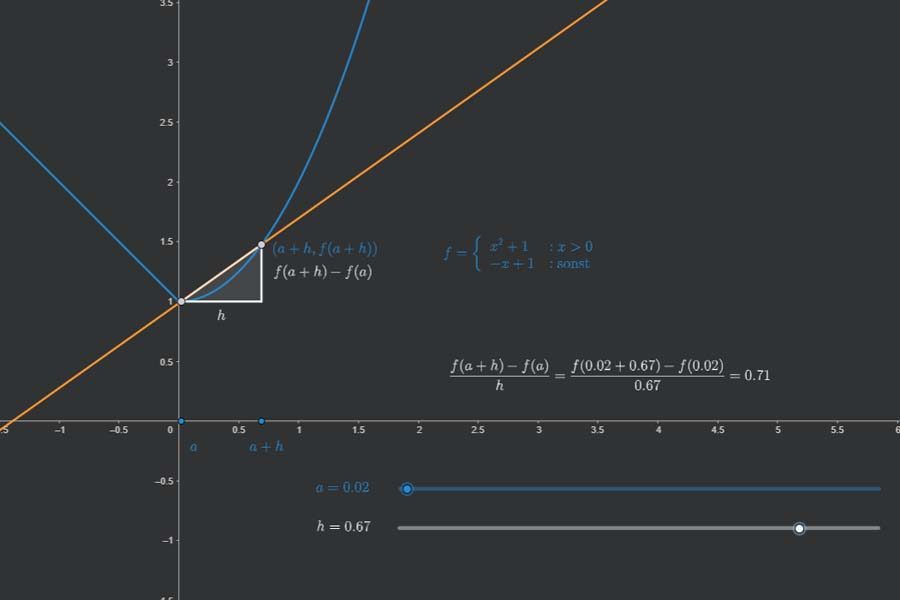
Die Ableitung einer Funktion an einem Punkt ist nichts anderes die Steigung der Tangenten an die Funktion in diesem Punkt und kann daher auch als „lokale Änderungsrate“ der Funktion aufgefasst werden. Das ist ziemlich bekannt. Wie aber berechnet man überhaupt die Tangente und damit ihre Steigung mathematisch präzise? Das geht nur über Folgen von „Hilfsgeraden“ und ihre Grenzwerte. Diese Erkenntnis und das Vorgehen können es an Wichtigkeit locker mit der Erfindung des Computers aufnehmen.

Differentiation: Derivatives and Tangents

Wähle mit dem blauen Schieberegler den Punkt a auf der x-Achse, an dem die Ableitung unserer Beispielfunktion (f(x)=x^2) berechnet werden soll. Die Grafik illustriert die Ermittlung der Ableitung als Grenzwert von Folgen aus Sekantensteigungen (=Quotient aus vertikaler und horizontaler Kathete des gelben Steigungsdreiecks). Dieser Grenzwert wird auch Differentialquotient genannt. Mit dem gelben Schieberegler kannst Du den Wert h wählen, der den Punkt (a+h,f(a+h)) festlegt, welcher neben dem Basispunkt (a,f(a)) den zweiten Punkt definiert, durch den die Sekanten (orangefarbene Geraden) verlaufen. Die gelb dargestellten Berechnungen zeigen, wie die Ableitung letztlich über den Begriff des Grenzwertes einer Folge konkret berechnet wird.

Hier sind alle harten und trockenen Apps zum Thema. Schau mal rein!

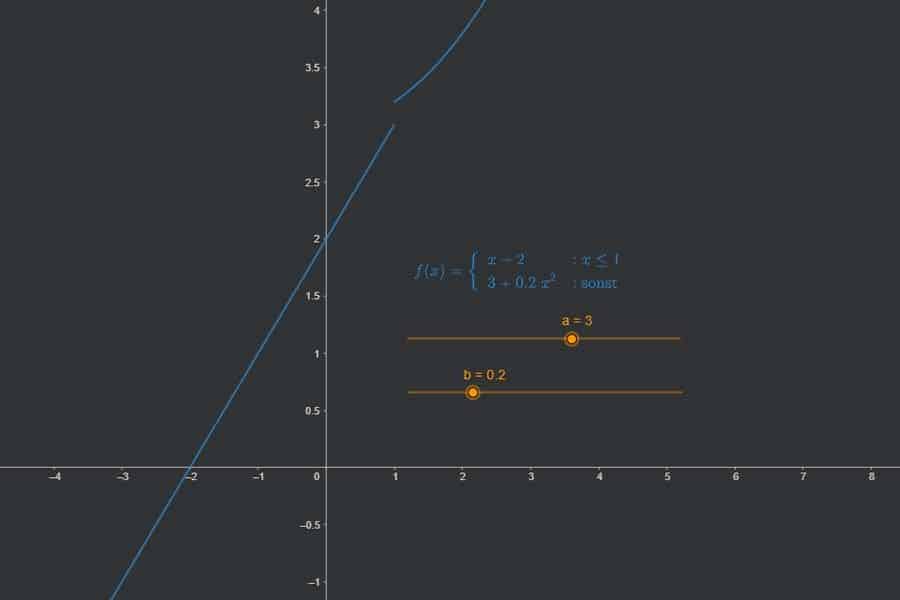
Interaktiv: Ableitung der Umkehrfunktion

Differentialrechnung

Funktion in Spiegelschrift. Ableitung in Spiegelschrift. Mit Bild ist die Lösung so einfach.

Interaktiv: Arithmetische Folge und Reihe

Finanzmathematik

Weihnachtsferien: Jeden Tag ein halbes Kilo zunehmen. Diese Folge kennt das Problem.

Interaktiv: Geometrische Folge und Reihe

Finanzmathematik

Die geometrische Folge beschreibt Wachstumsprozesse mit konstantem Wachstumsfaktor.

Interaktiv: Einfache Zinseszinsrechnung

Finanzmathematik

Wir legen Geld an bei fester Verzinsung. Wie viel Geld haben wir nach n Jahren?

Interaktiv: Zinseszinsrechnung bei jährlicher konstanter Einzahlung

Finanzmathematik

Wir sparen! Jährlich denselben Betrag bei fester Verzinsung. Was haben wir am Ende?

Interaktiv: Berechnung der Ableitung mit dem Differentialquotienten

Differentialrechnung

Kern der Differentialrechnung. Locker mit der Erfindung des Computers vergleichbar.

Interaktiv: Links- und rechtsseitige Ableitung

Differentialrechnung

Halbe Sachen machen: Differenzierbarkeit von links oder rechts.

Interaktiv: Eine besondere Folge

Finanzmathematik

Die Eulersche Zahl e. Immer und immer wieder taucht sie auf. Warum eigentlich?

Interaktiv: Stetigkeit

Folgen und Reihen

Stetigkeit mit Folgen. Und zwar ernsthaften. Und das kann auch schiefgehen.

Interaktiv: Beispiel Stetigkeit und Differenzierbarkeit

Differentialrechnung

Stetig heißt: kein Sprung. Differenzierbar heißt: kein Knick. So einfach ist das. Meistens.