Komplexe Zahlen sind Punkte in einer Ebene. Punkte kann man darstellen in „kartesischen“ Koordinaten („gehe soundso viel horizontal und soundso viel vertikal“) oder in „Winkel-Radius-Darstellung“ („Dreh dich um diesen Winkel und gehe dann soundso weit in gerader Richtung“). Genauso kann man mit komplexen Zahlen verfahren. Und beide Darstellungen haben ihre Vor- und Nachteile – je nach Situation.
Bewege die komplexe Zahl c (weißer Punkt). Beobachte dabei, wie sich Realteil, Imaginärteil (blau) sowie Winkel und Radius (orange) entsprechend verändern. Realteil und Imaginärteil sind die Bestandteile der sogenannten kartesischen Darstellung von c (linker Teil der weißen Formel); Winkel und Radius sind die Bestandteile sowohl der Polardarstellung (mittlerer Teil der weißen Formel) als auch der Eulerschen Darstellung (rechter Teil der weißen Formel) von c. In der Polardarstellung wird der Winkel typischerweise in Graddarstellung, in der Eulerdarstellung in Bogenmaß-Darstellung verwendet. Die drei Darstellungen lassen sich leicht ineinander umrechnen (siehe Videos).
Hier sind alle harten und trockenen Apps zum Thema. Schau mal rein!
Wie hätten Sie Ihre komplexe Zahl gern? Kartesisch, polar oder nach Euler-Art? Wir haben alles.
Kinderleicht. Wenn beide Zahlen kartesisch vorliegen. Sonst: kartesisch machen. Klar!? Klar.
Komplexe Zahlen zu multiplizieren ist schwieriger zu schreiben als zu machen. Ehrlich.
Teile und herrsche! Heißt es. Aber erstmal: Beherrsche teilen! Keine Angst: nicht schwierig.
Jede komplexe Zahl hat n verschiedene n-te Wurzeln, angeordnet wie auf einer Torte. Hurra!
Komplexes potenzieren? Klingt anstrengend. Ist es aber nicht. Im Gegenteil.
Viele sprechen darüber, wenige durchschauen sie: Neuronale Netze. Wir schaffen Durchblick.
www.hartundtrocken.de
Die App visualisiert ein einfaches neuronales Netz – wie es lernt und wie es arbeitet – am Beispiel der Erkennung handgeschriebener Ziffern. Diese können mit der Maus live auf ein einfaches Zeich...Interaktiv: Der K-Nearest-Neighbours-Algorithmus
www.hartundtrocken.de
“kNN” steht für “k nearest neighbours”. Der kNN-Algorithmus ist ein einfach zu verstehender Vertreter der “supervised” Machine-Learning-Algorithmen: Ein neuer Datenpunkt (weiß) wird vom ...👏 "Wie war das mit dem Bauchfett? Dein Mathelehrer wird dich hassen für diesen uralten Trick😜" 😂😂😂
© 2020-2023 Hart und Trocken | Impressum | Datenschutz | Coverband Stuttgart
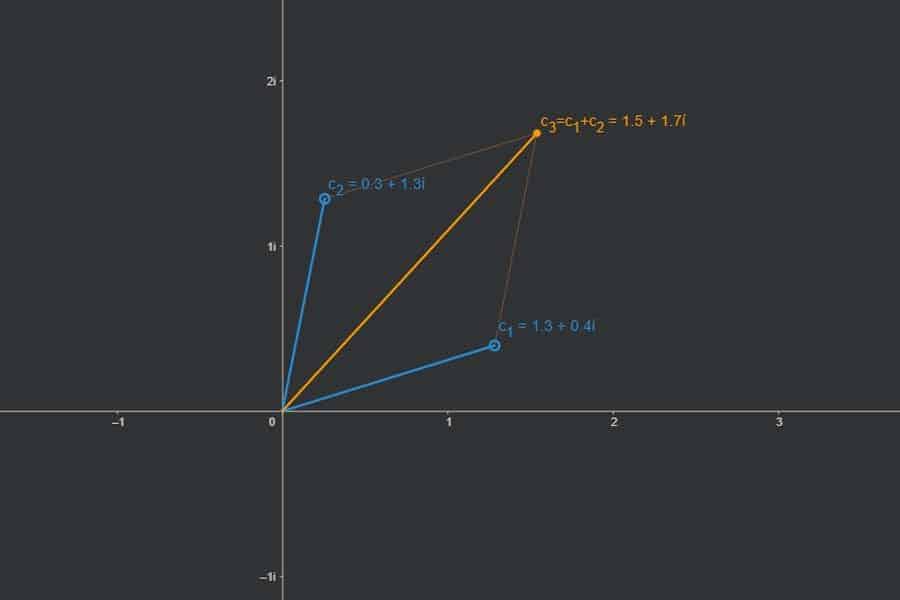
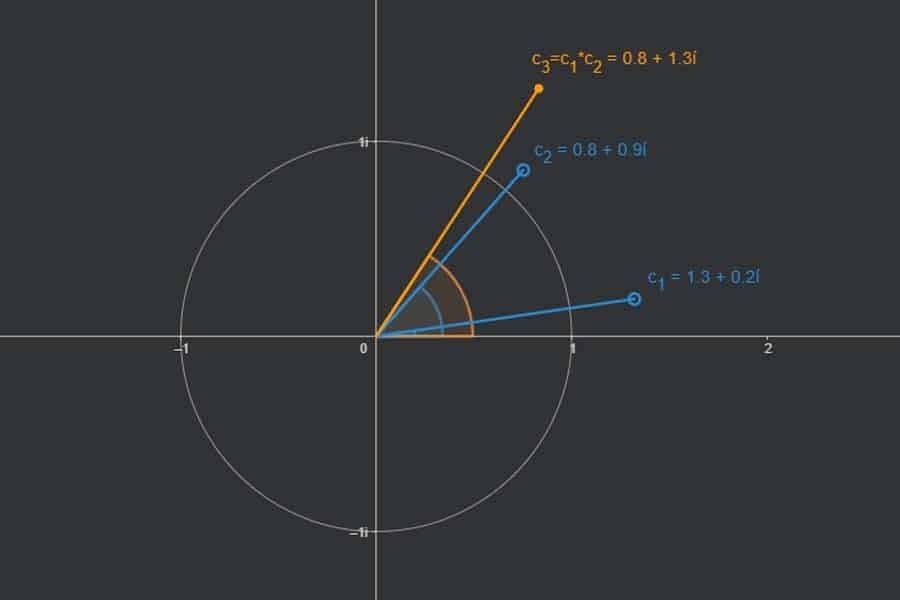
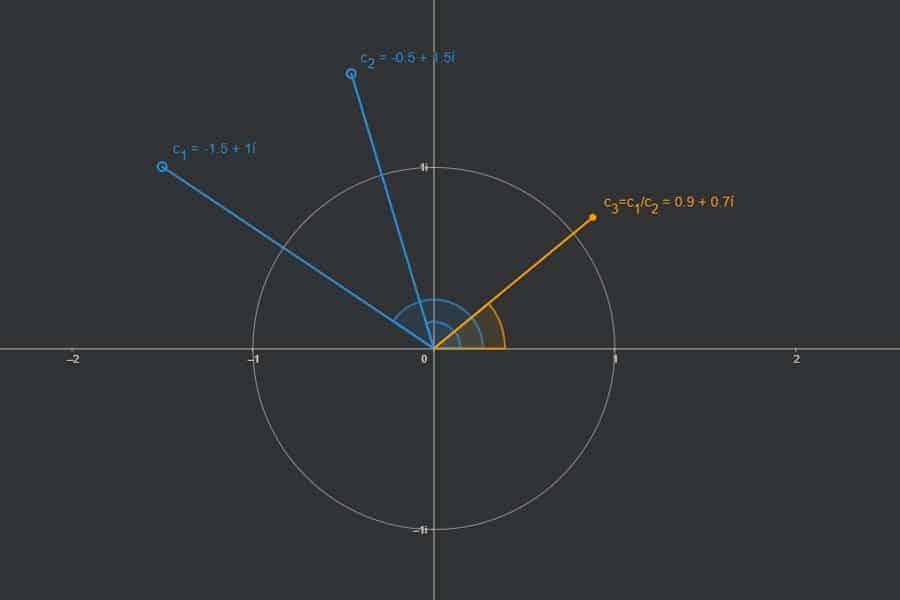
Interaktiv: Darstellungen komplexer Zahlen