Wir wollen eine komplexe Zahl durch eine andere teilen. Das geht sowohl in kartesischer, als auch in Radius-Winkel-Darstellung (Polardarstellung und Euler-Darstellung). Wobei die beiden Vorgehensweisen komplett verschieden sind. Macht nichts, beide sind nicht wirklich schwierig, und nach zweimal Üben hat man’s drauf.
Bewege die komplexen Zahlen c1 und c2 (blaue Punkte). Beobachte dabei, wie sich die Position der komplexen Zahl c3, der Quotient aus c1 und c2 (orangefarbener Punkt), entsprechend ändert. Geometrisch ergibt sich der Quotient c3, indem der Radius von c1 durch den von c2 dividiert wird und vom Winkel von c1 der Winkel von c2 subtrahiert wird. Wie sich der „orangefarbene“ Winkel als Differenz der beiden „blauen“ Winkel ergibt, kann man am besten beobachten, wenn c1 und c2 auf dem Einheitskreis (Kreis mit Radius 1 um den Ursprung) liegen, da die Radien dann alle 1 sind.
Hier sind alle harten und trockenen Apps zum Thema. Schau mal rein!
Wie hätten Sie Ihre komplexe Zahl gern? Kartesisch, polar oder nach Euler-Art? Wir haben alles.
Kinderleicht. Wenn beide Zahlen kartesisch vorliegen. Sonst: kartesisch machen. Klar!? Klar.
Komplexe Zahlen zu multiplizieren ist schwieriger zu schreiben als zu machen. Ehrlich.
Teile und herrsche! Heißt es. Aber erstmal: Beherrsche teilen! Keine Angst: nicht schwierig.
Jede komplexe Zahl hat n verschiedene n-te Wurzeln, angeordnet wie auf einer Torte. Hurra!
Komplexes potenzieren? Klingt anstrengend. Ist es aber nicht. Im Gegenteil.
Viele sprechen darüber, wenige durchschauen sie: Neuronale Netze. Wir schaffen Durchblick.
www.hartundtrocken.de
Die App visualisiert ein einfaches neuronales Netz – wie es lernt und wie es arbeitet – am Beispiel der Erkennung handgeschriebener Ziffern. Diese können mit der Maus live auf ein einfaches Zeich...Interaktiv: Der K-Nearest-Neighbours-Algorithmus
www.hartundtrocken.de
“kNN” steht für “k nearest neighbours”. Der kNN-Algorithmus ist ein einfach zu verstehender Vertreter der “supervised” Machine-Learning-Algorithmen: Ein neuer Datenpunkt (weiß) wird vom ...👏 "Wie war das mit dem Bauchfett? Dein Mathelehrer wird dich hassen für diesen uralten Trick😜" 😂😂😂
© 2020-2023 Hart und Trocken | Impressum | Datenschutz | Coverband Stuttgart
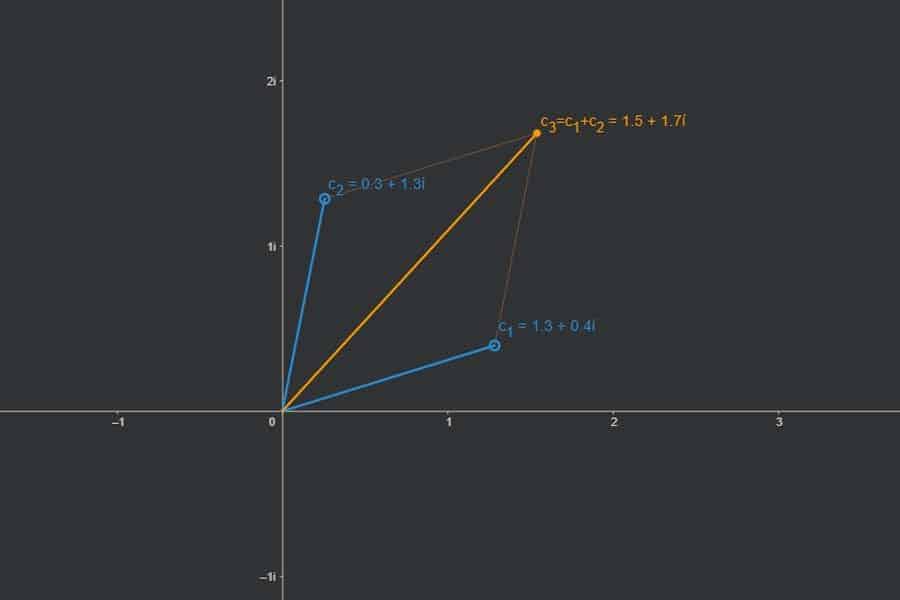
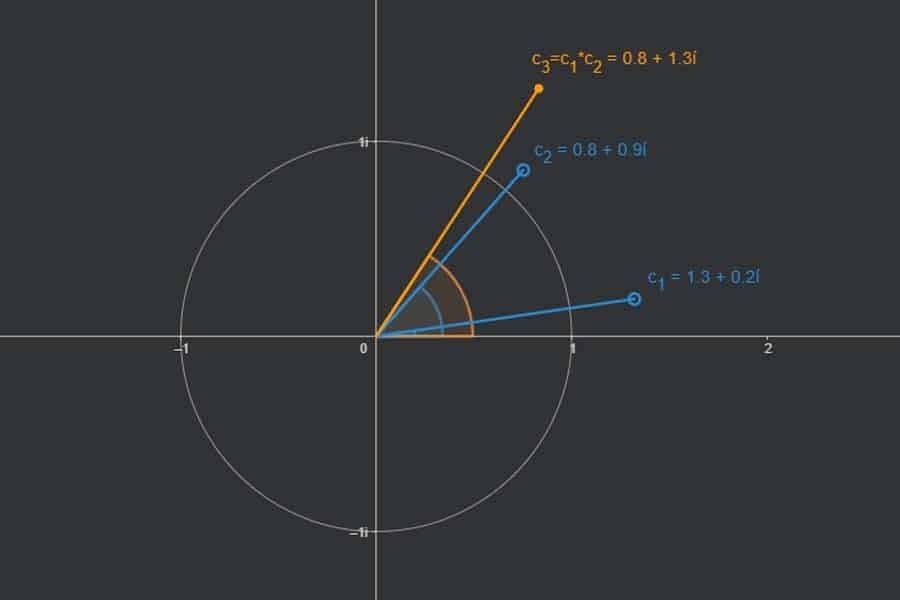
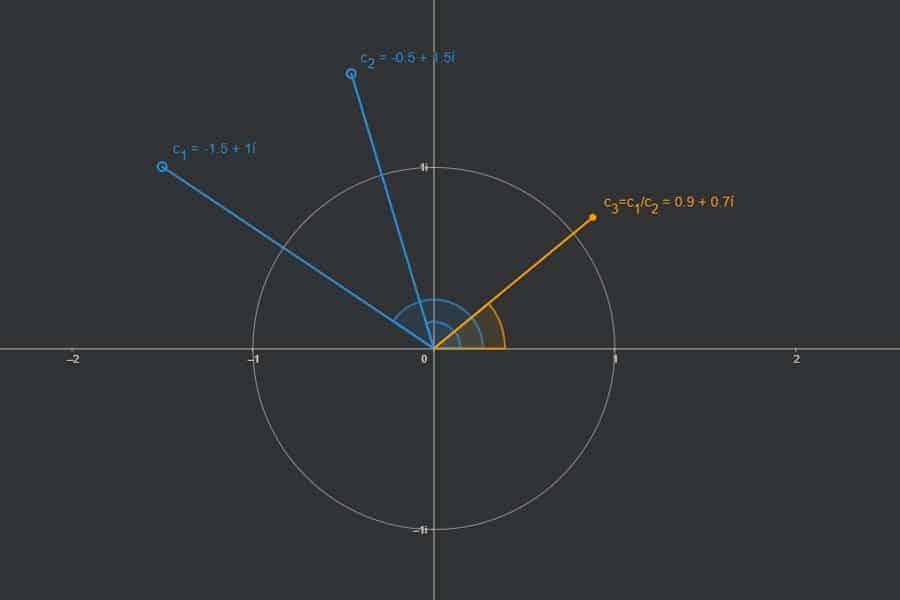
Interaktiv: Darstellungen komplexer Zahlen