Bastelstunde! Wir schrauben periodische Funktionen aus Einzelschwingungen zusammen.
Fourier-Reihe der Sägezahnfunktion? Hart? Auf jeden Fall. Hier wird veranschaulicht, wie sich die Fourier-Reihe Schritt für Schritt als Funktion aufbaut und dabei der Sägezahnkurve immer ähnlicher wird.


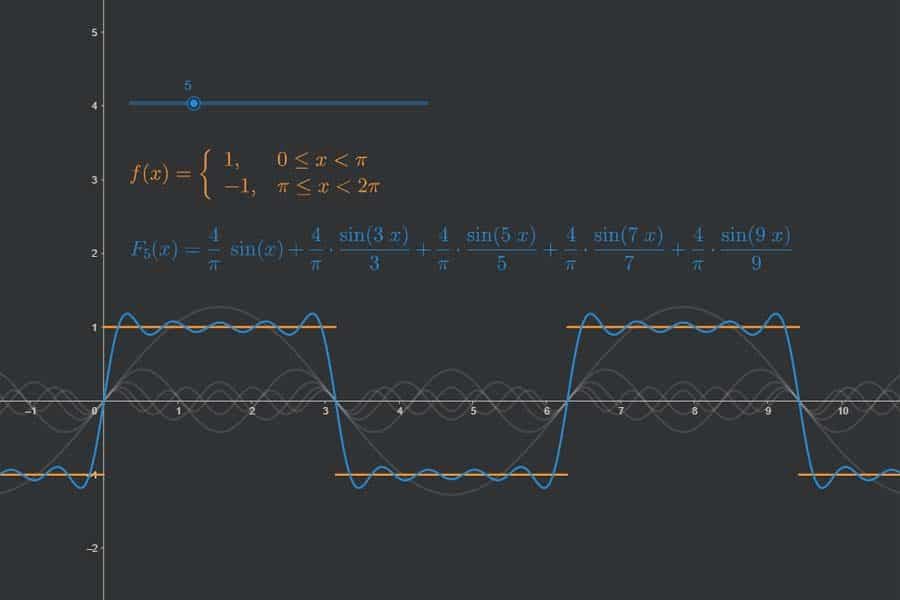
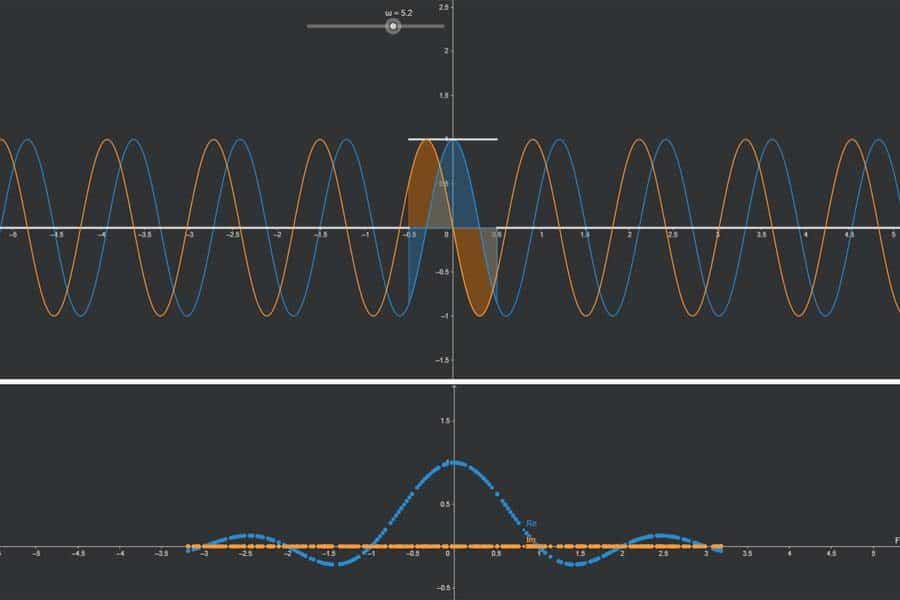
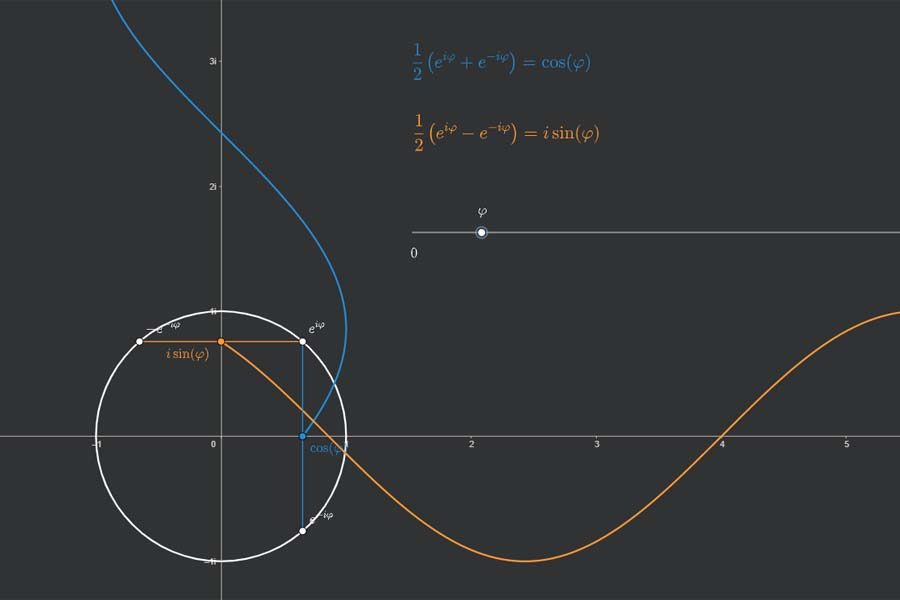
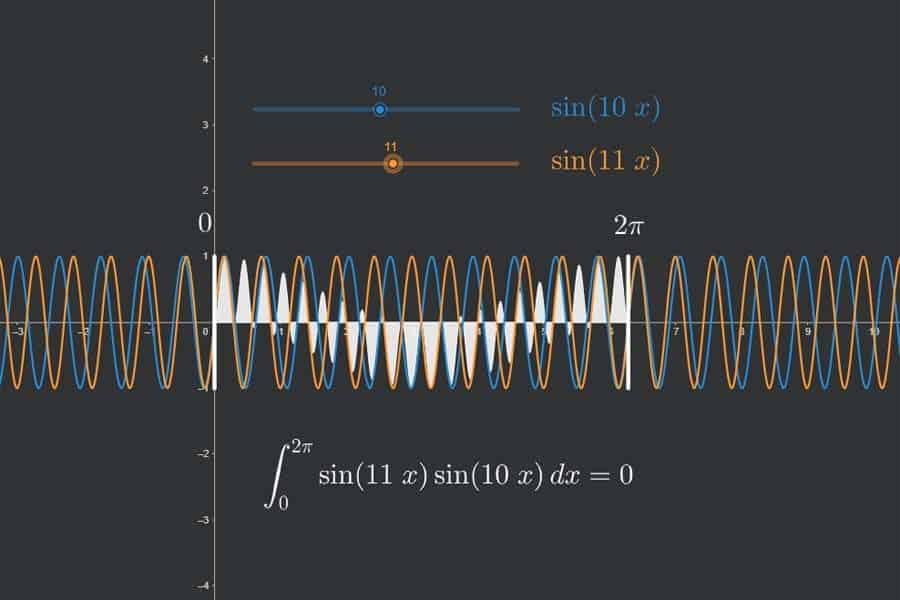
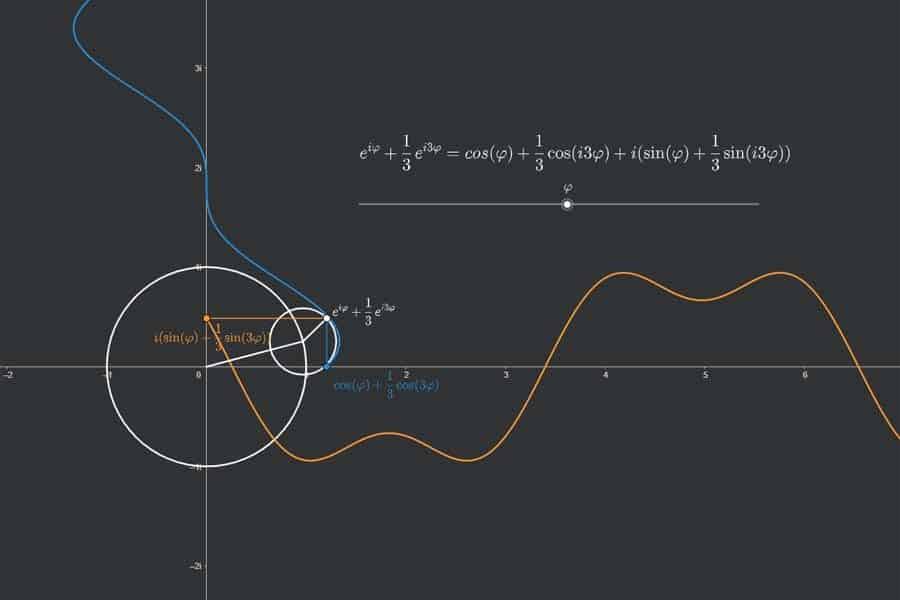
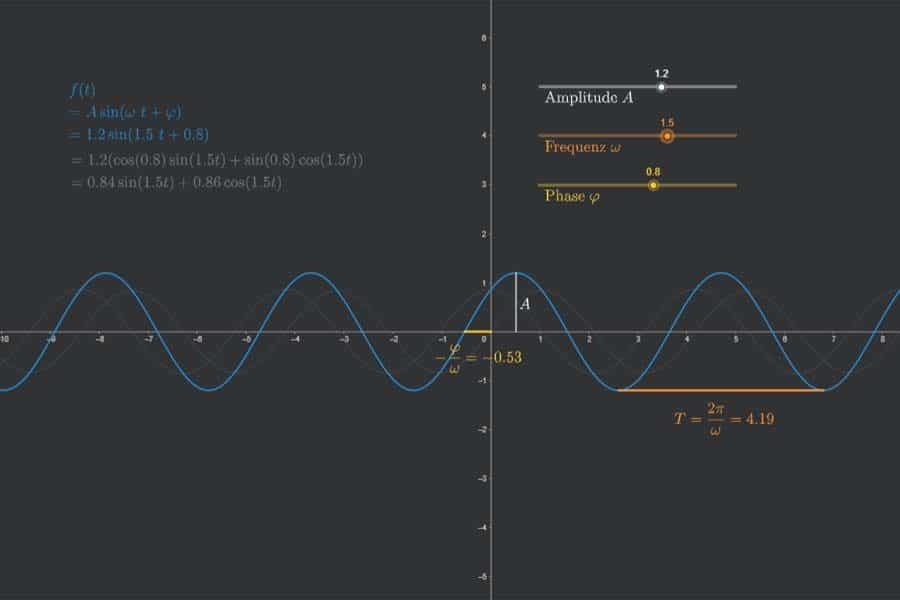
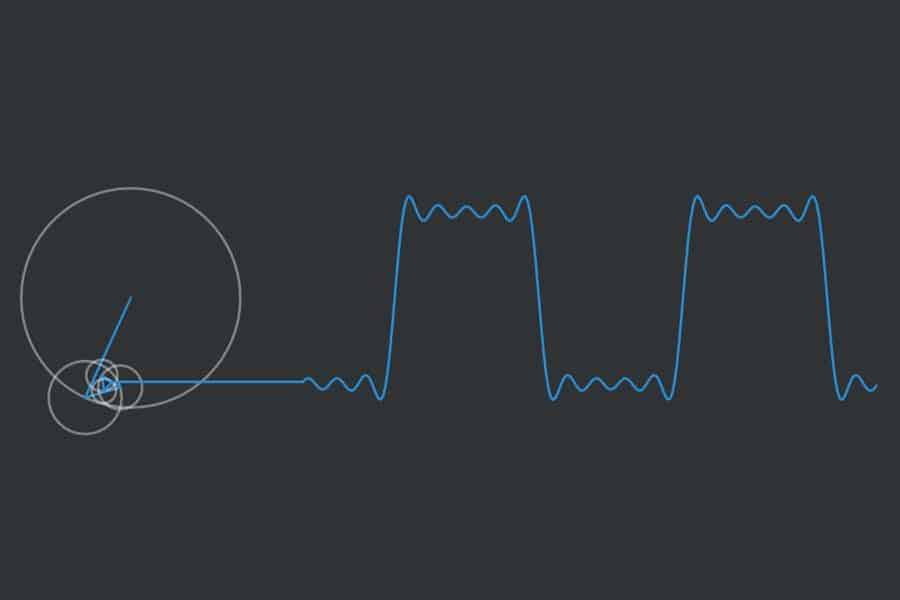












Interaktiv: Fourier-Synthese