Weihnachtsferien: Jeden Tag ein halbes Kilo zunehmen. Diese Folge kennt das Problem.
Die geometrische Folge beschreibt Wachstums- oder Zerfallsprozesse mit konstantem Wachstums- bzw. Schrumpfungsfaktor, was man auch als diskretes exponentielles Wachstum bezeichnen kann (wobei „diskret“ soviel bedeutet wie „ohne Zwischenschritte“). Beispiele sind Verzinsung von Kapital (mit Zinseszinsen) oder Infektionszahlen in einer Pandemie. Die geometrische Reihe basiert auf der geometrischen Folge und ist nichts anders als die Folge der sogenannten Partialsummen (also der ersten n Folgenglieder). Bisschen verwirrend, aber überhaupt nicht schwer, wenn man es mal begrifflich sortiert hat.


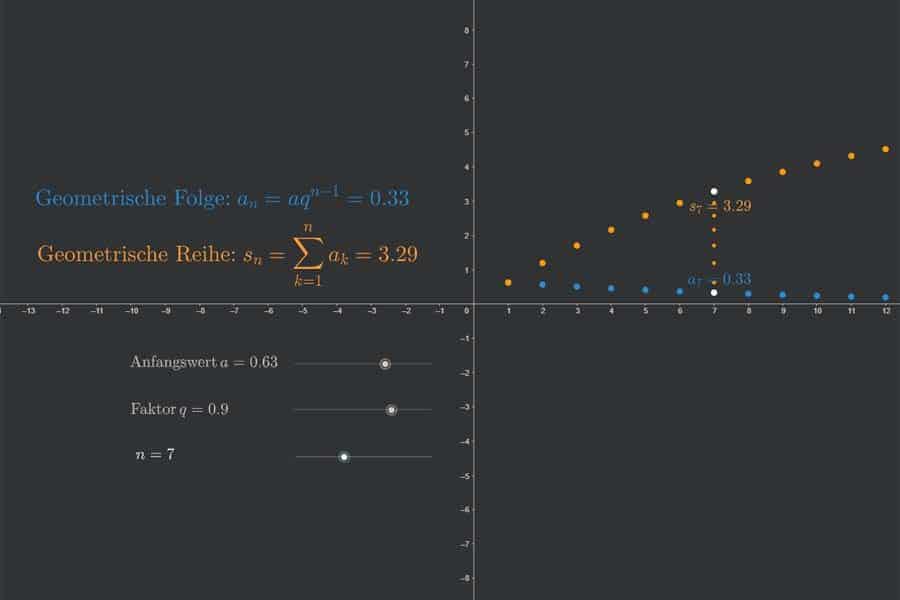
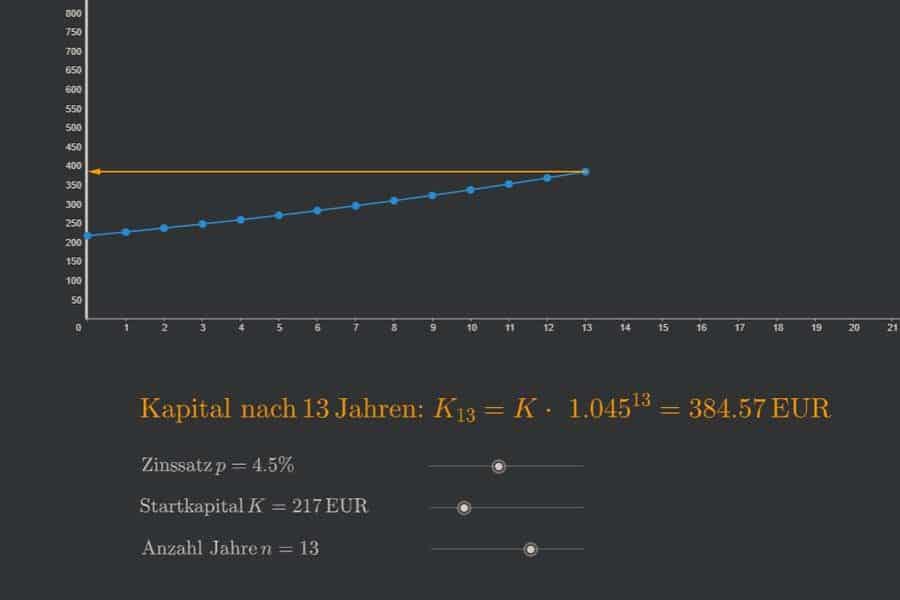
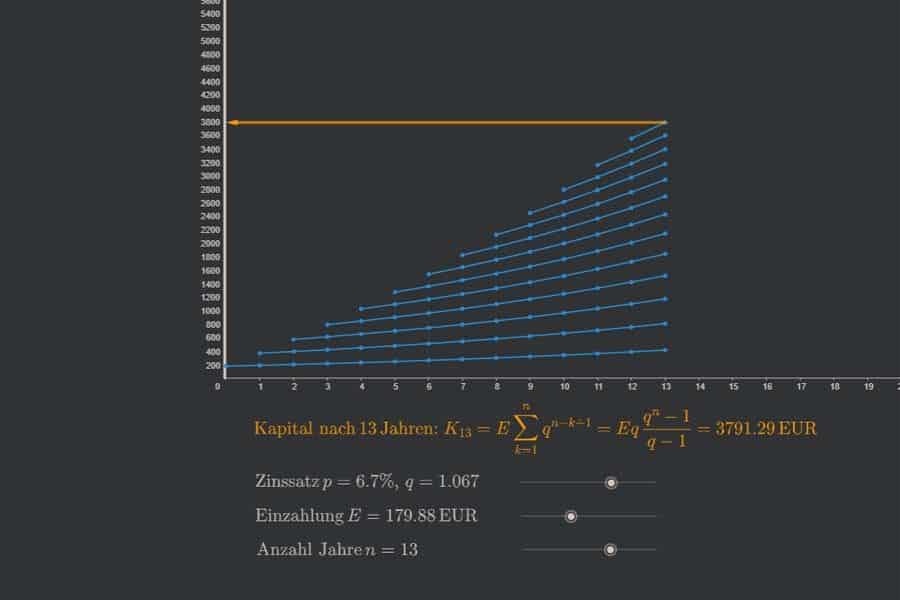
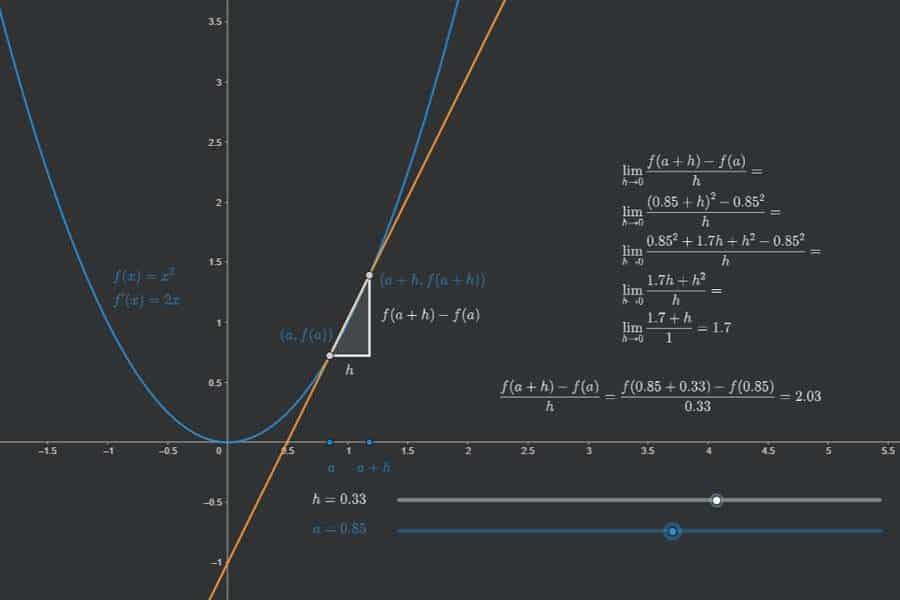











Interaktiv: Arithmetische Folge und Reihe