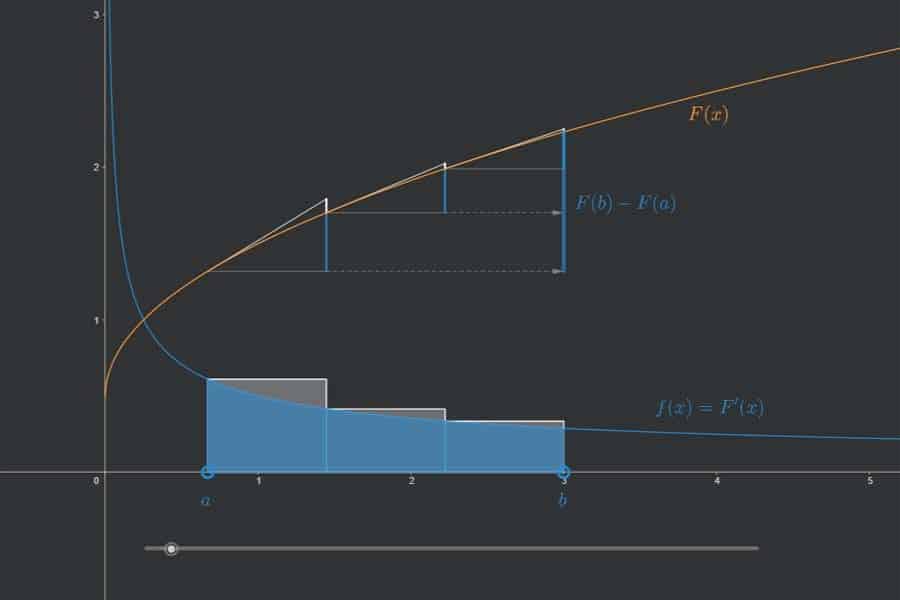
Bewege den Schieberegler, um die Position des Punktes a auf der x-Achse zu verändern. Die weiße Funktion F ist die Verkettung der blauen Funktion f und der orangefarbenen Funktion g. Die Kettenregel besagt, dass sich die Ableitung der verketteten (=weißen) Funktion F als Produkt aus den Ableitungen der (blauen) Funktion f und der (orangefarbenen) Funktion g ergibt (hierbei ist wichtig zu realisieren, dass diese drei Ableitungen an den „richtigen“ Punkten betrachtet werden müssen, d. h. für f am Punkt a, für g am Punkt f(a), für F wiederum am Punkt a). Diese Ableitungen werden durch die vertikalen Seiten der drei eingezeichneten Steigungsdreiecke repräsentiert. Man kann leicht nachvollziehen, dass die Kettenregel „stimmt“, d. h. dass sich die Länge der vertikalen Seite im weißen Dreieck (für F) als Produkt aus den Längen der vertikalen Seiten im blauen (für f) und im orangefarbenen Dreieck (für g) ergibt.


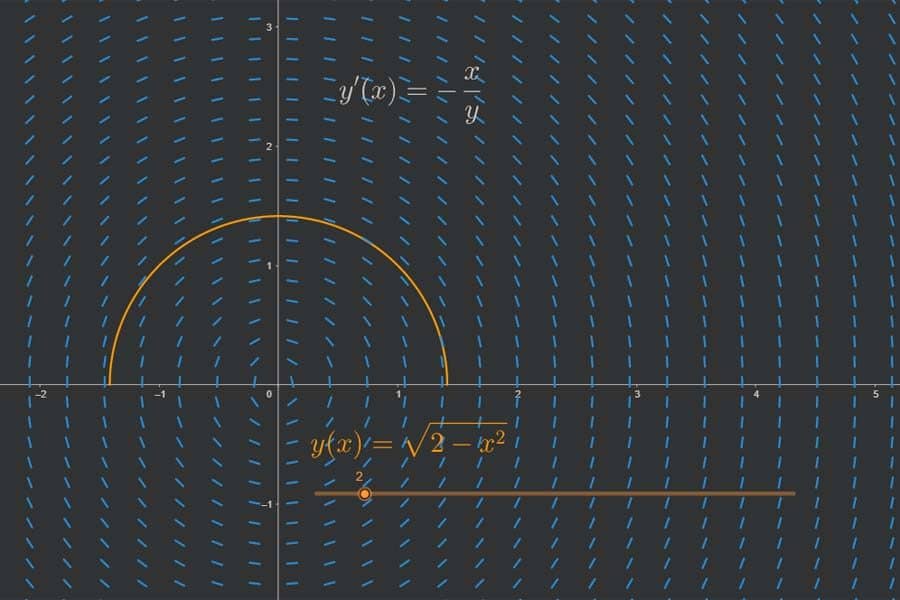
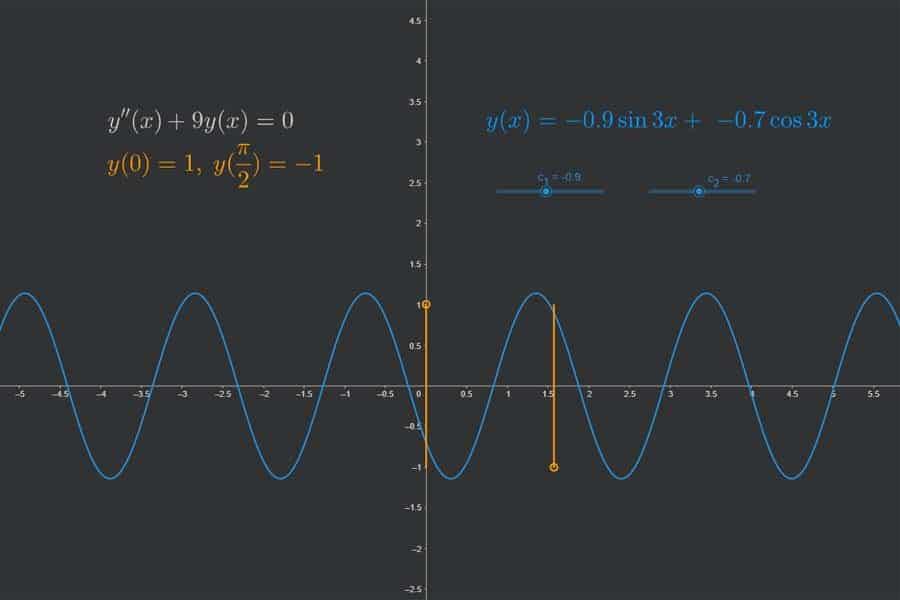

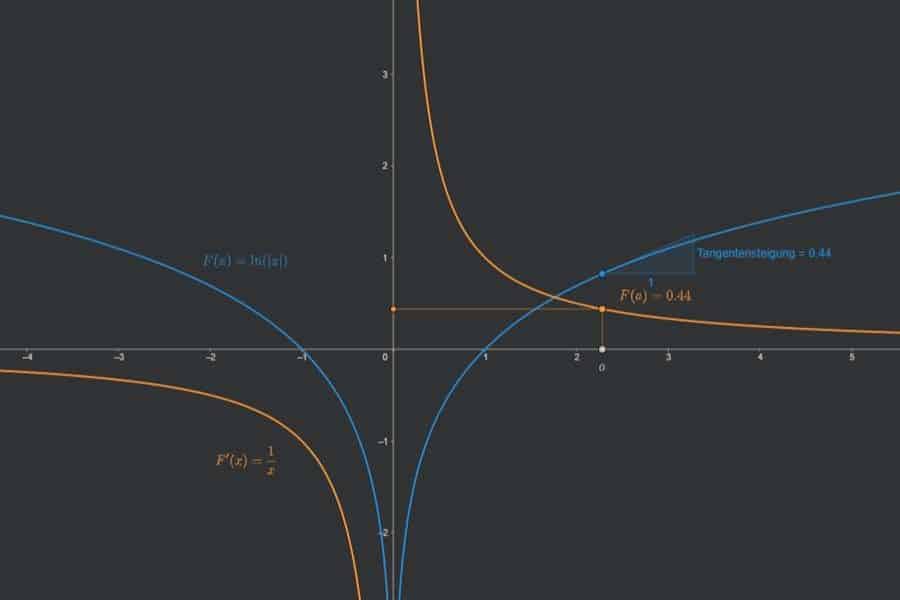
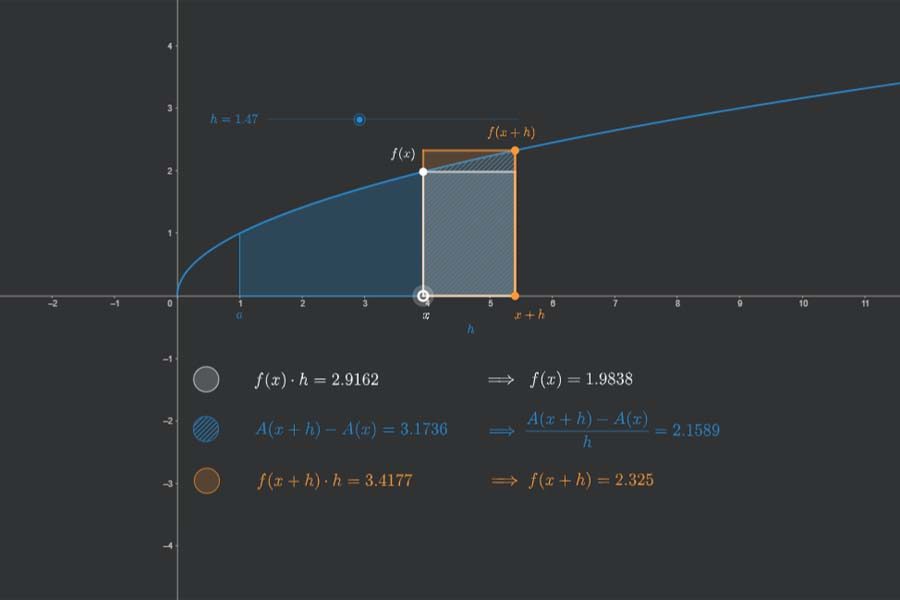











Interaktiv: Richtungsfeld und Trajektorien einer Differentialgleichung