Zerlegung eines Vektors in Bestandteile vorgegebener Richtungen
Wenn man zwei Richtungen in der Ebene mittels zweier Vektoren vorgibt (hier: blau und orangefarben), dann kann man versuchen, einen beliebigen dritten Vektor (hier: weiß) in seine Komponenten dieser beiden Richtungen zu zerlegen. Anders ausgedrückt: man stellt ihn als Summe geeigneter Vielfacher der Ausgangsvektoren dar (so genannte Linearkombination). Um diese geeigneten Vielfachen und damit die Linearkombination zu finden, muss ein lineares Gleichungssystem gelöst werden.


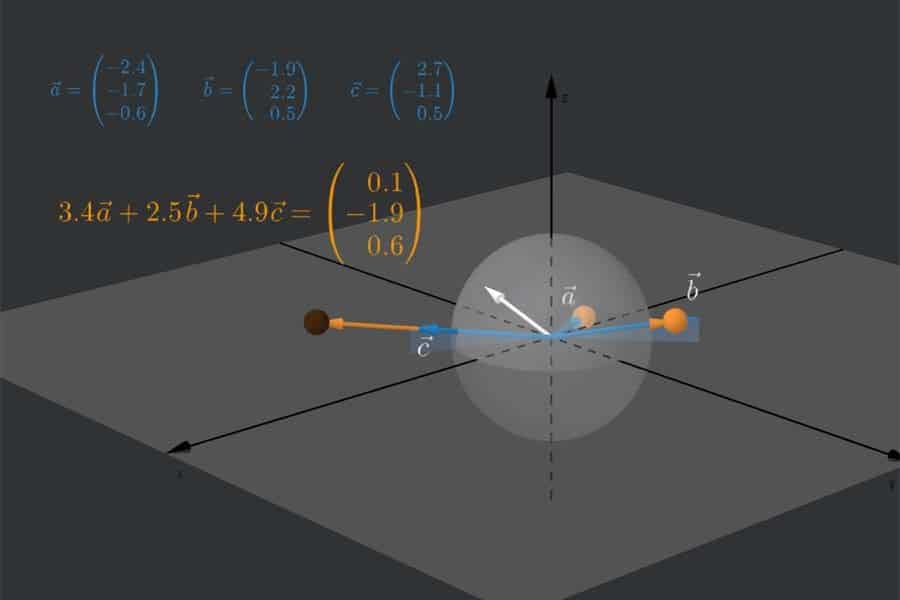
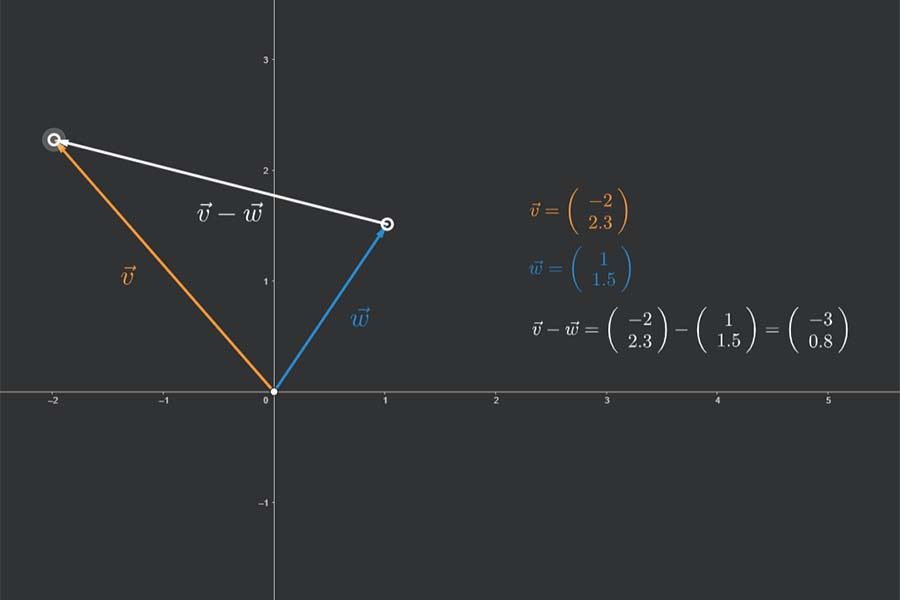

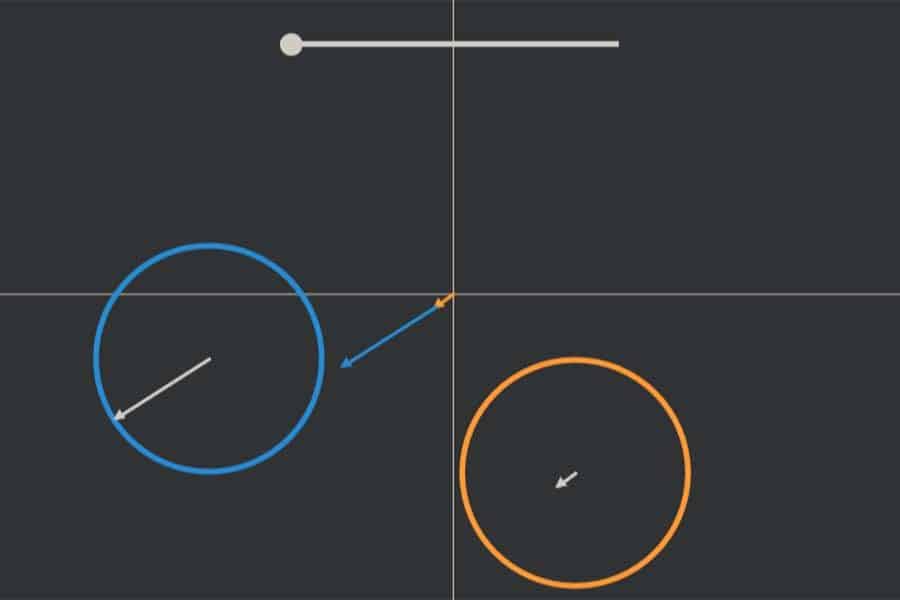
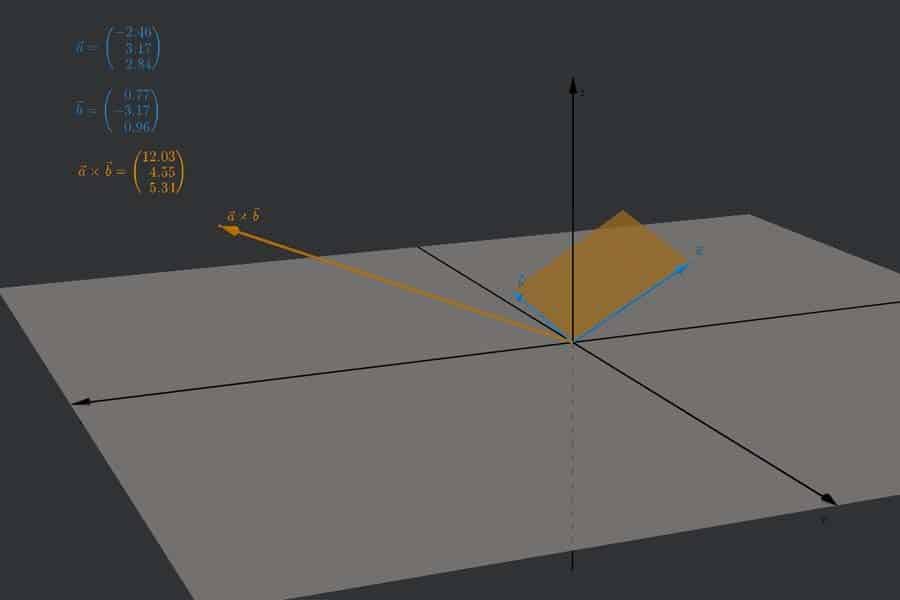











Interaktiv: Komponentenzerlegung von 2D-Vektoren