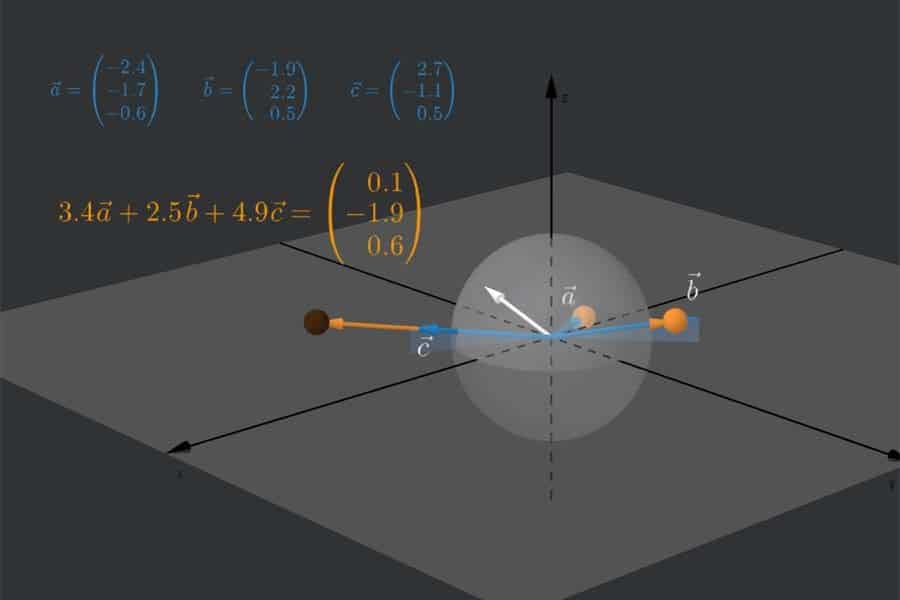
Spielregel: Versuche, die drei orangefarbenen Punkte so zu verschieben, dass der weiße Vektor und die dazugehörige Kugel auf Null zusammenschrumpft (so wie im Ausgangszustand der Fall). Wenn das nur gelingt, indem du alle drei Punkte exakt in den Nullpunkt (Schnittpunkt der Achsen) setzt, dann sind die drei blauen Vektoren \vec{a},\;\vec{b} und \vec{c} linear unabhängig (d. h. sie lassen sich nicht als Linearkombinationen aus den jeweils anderen konstruieren). Wenn es allerdings zusätzlich auch in einer anderen Variante gelingt, die Kugel auf Null schrumpfen zu lassen, dann sind die blauen Vektoren linear abhängig (was seltener geschieht). In diesem Fall lässt sich mindestens einer von ihnen als Linearkombination aus den jeweils anderen konstruieren. Das ist bei drei Vektoren genau dann der Fall, wenn alle in einer gemeinsamen Ebene liegen.
Hinweis: Beim Aufrufen der Seite (bzw. Neuladen) sind die blauen Vektoren so positioniert, dass sie linear abhängig sind, was man daran sieht, dass die Kugel nicht zu sehen (auf Null geschrumpft) ist. Die Vektoren lassen sich bewegen, indem du die orangefarbenen Punkte einmal (Horizontalbewegung) oder zweimal (Vertikalbewegung) anklickst und dann mit der Maus verschiebst.



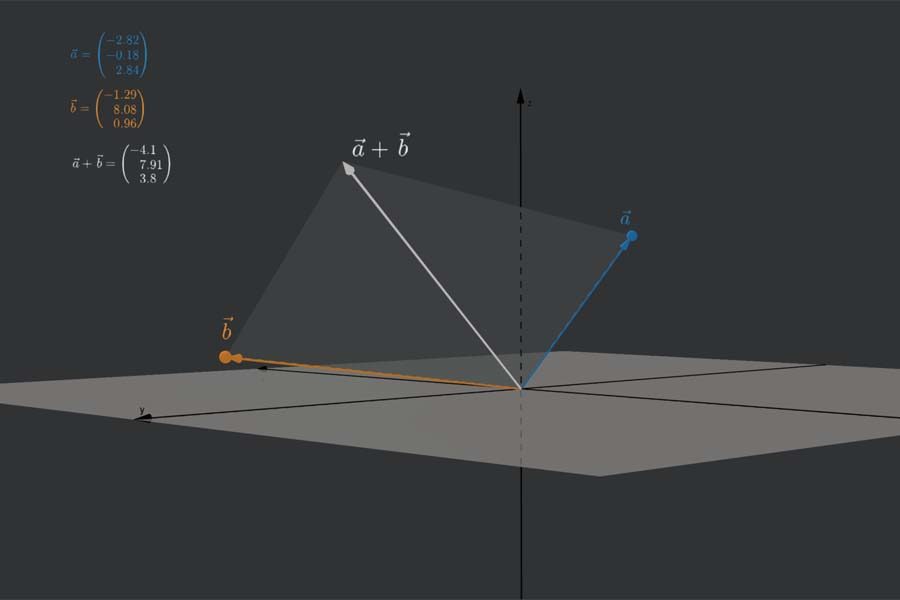











Interaktiv: Komponentenzerlegung von 2D-Vektoren