Potenzen von komplexen Zahlen lassen sich leichter ausrechnen, als man das auf den ersten Blick denkt. Sofern sie in Euler- oder Polarform vorliegen. Falls nicht, muss man sie in eine dieser beiden Formen bringen.
Bewege die komplexe Zahl z (blauer Punkt) und wähle mit dem Schieberegler für n einen Wert zwischen 1 und 50. Die orangefarbenen komplexen Zahlen sind dann die Folge der komplexen Potenzen von z (von der ersten, d. h. z selbst, bis zur n-ten). Wie lautet der „Konstruktionsplan“ für diese Potenzen? Einfach:
Hier sind alle harten und trockenen Apps zum Thema. Schau mal rein!
Wie hätten Sie Ihre komplexe Zahl gern? Kartesisch, polar oder nach Euler-Art? Wir haben alles.
Kinderleicht. Wenn beide Zahlen kartesisch vorliegen. Sonst: kartesisch machen. Klar!? Klar.
Komplexe Zahlen zu multiplizieren ist schwieriger zu schreiben als zu machen. Ehrlich.
Teile und herrsche! Heißt es. Aber erstmal: Beherrsche teilen! Keine Angst: nicht schwierig.
Jede komplexe Zahl hat n verschiedene n-te Wurzeln, angeordnet wie auf einer Torte. Hurra!
Komplexes potenzieren? Klingt anstrengend. Ist es aber nicht. Im Gegenteil.
Viele sprechen darüber, wenige durchschauen sie: Neuronale Netze. Wir schaffen Durchblick.
www.hartundtrocken.de
Die App visualisiert ein einfaches neuronales Netz – wie es lernt und wie es arbeitet – am Beispiel der Erkennung handgeschriebener Ziffern. Diese können mit der Maus live auf ein einfaches Zeich...Interaktiv: Der K-Nearest-Neighbours-Algorithmus
www.hartundtrocken.de
“kNN” steht für “k nearest neighbours”. Der kNN-Algorithmus ist ein einfach zu verstehender Vertreter der “supervised” Machine-Learning-Algorithmen: Ein neuer Datenpunkt (weiß) wird vom ...👏 "Wie war das mit dem Bauchfett? Dein Mathelehrer wird dich hassen für diesen uralten Trick😜" 😂😂😂
© 2020-2023 Hart und Trocken | Impressum | Datenschutz | Coverband Stuttgart
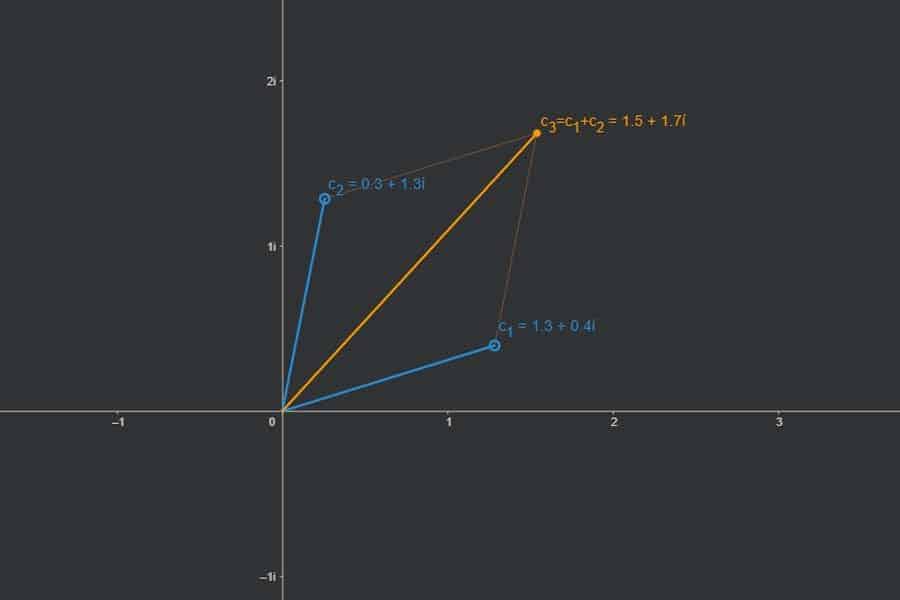
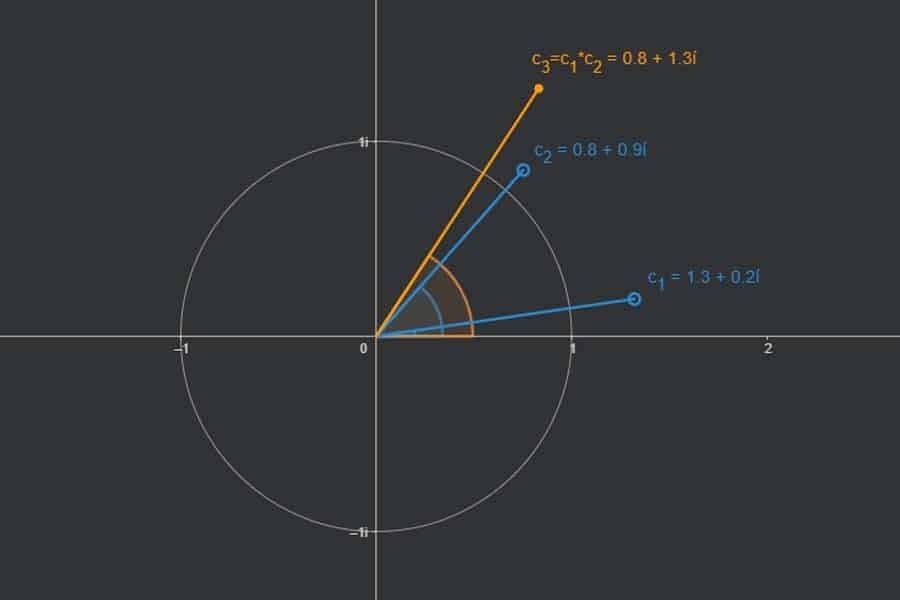
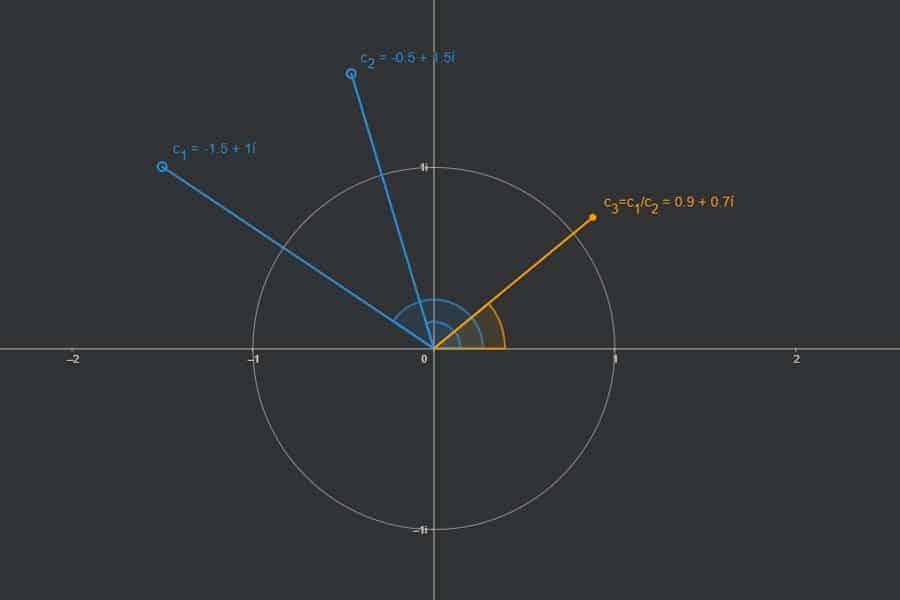
Interaktiv: Darstellungen komplexer Zahlen