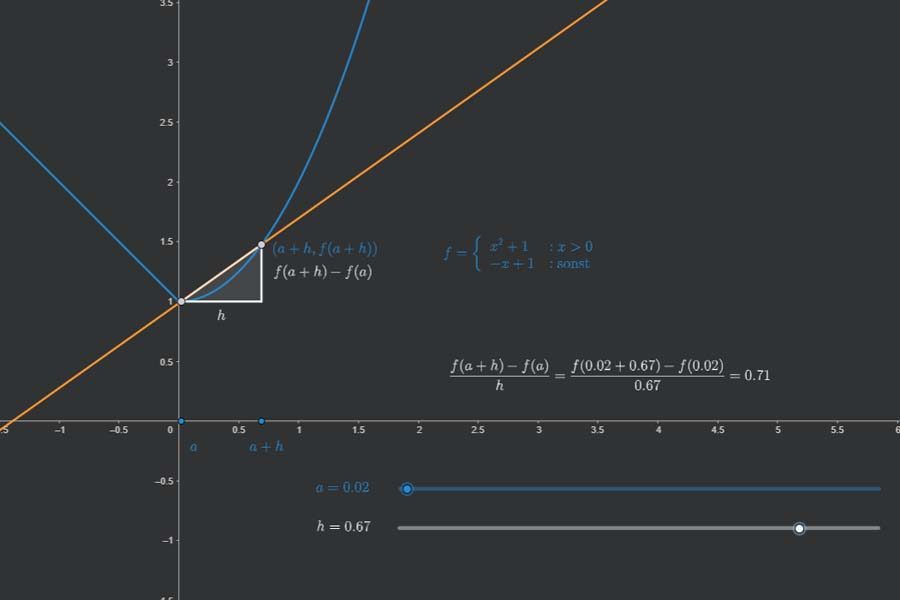
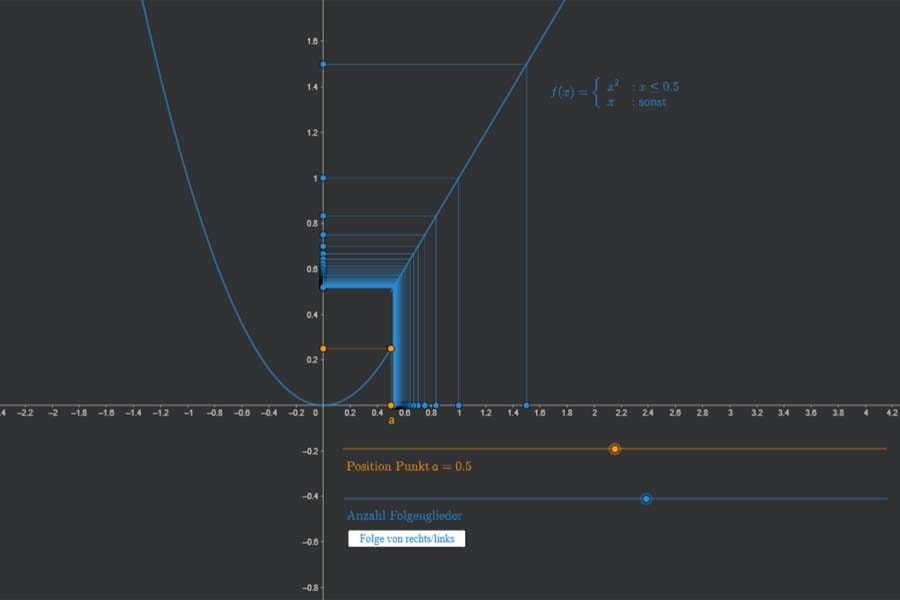
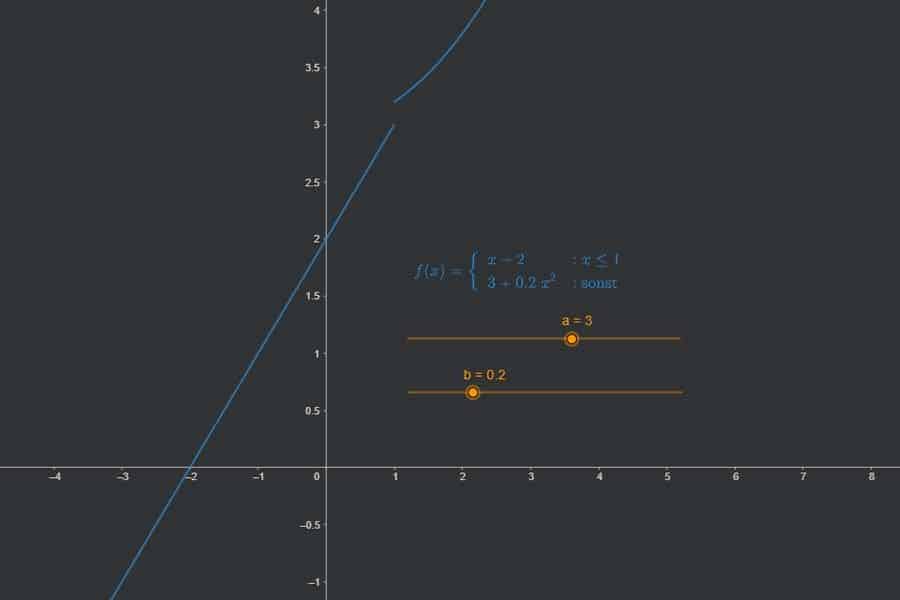
„Stetig“ heißt, den Funktionsgraph ohne Unterbrechung mit einem Stift zeichnen zu können. Zumindest in den meisten Fällen. Mathematisch sauber aber wird Stetigkeit über Folgen definiert: Für jede Folge auf der x-Achse, die gegen einen Punkt a auf der x-Achse konvergiert, muss die zugehörige Bildfolge unter der Funktion f gegen den Funktionswert f(a) konvergieren. Schauen wir uns das mal genauer an.
Wähle mit dem orangefarbenen Schieberegler den Punkt a auf der x-Achse, an die Stetigkeit der Beispielfunktion mittels des Folgenkriteriums überprüft werden soll. Lasse dann mit dem blauen Schieberegler eine Folge auf der x-Achse gegen den Punkt a konvergieren und beobachte, ob die Folge der Funktionswerte gegen f(a) konvergiert. Die Funktion f ist dann und nur dann am Punkt a stetig, wenn dies für alle möglichen Folgen, die gegen a konvergieren, der Fall ist. Wie sieht es bei a=0,5 aus?
Hier sind alle harten und trockenen Apps zum Thema. Schau mal rein!
Weihnachtsferien: Jeden Tag ein halbes Kilo zunehmen. Diese Folge kennt das Problem.
Die geometrische Folge beschreibt Wachstumsprozesse mit konstantem Wachstumsfaktor.
Wir legen Geld an bei fester Verzinsung. Wie viel Geld haben wir nach n Jahren?
Wir sparen! Jährlich denselben Betrag bei fester Verzinsung. Was haben wir am Ende?
Kern der Differentialrechnung. Locker mit der Erfindung des Computers vergleichbar.
Halbe Sachen machen: Differenzierbarkeit von links oder rechts.
Die Eulersche Zahl e. Immer und immer wieder taucht sie auf. Warum eigentlich?
Stetigkeit mit Folgen. Und zwar ernsthaften. Und das kann auch schiefgehen.
Stetig heißt: kein Sprung. Differenzierbar heißt: kein Knick. So einfach ist das. Meistens.
Integral rechnen? Stammfunktion! Was aber, wenn man keine Stammfunktion hat oder kennt?
Viele sprechen darüber, wenige durchschauen sie: Neuronale Netze. Wir schaffen Durchblick.
www.hartundtrocken.de
Die App visualisiert ein einfaches neuronales Netz – wie es lernt und wie es arbeitet – am Beispiel der Erkennung handgeschriebener Ziffern. Diese können mit der Maus live auf ein einfaches Zeich...Interaktiv: Der K-Nearest-Neighbours-Algorithmus
www.hartundtrocken.de
“kNN” steht für “k nearest neighbours”. Der kNN-Algorithmus ist ein einfach zu verstehender Vertreter der “supervised” Machine-Learning-Algorithmen: Ein neuer Datenpunkt (weiß) wird vom ...👏 "Wie war das mit dem Bauchfett? Dein Mathelehrer wird dich hassen für diesen uralten Trick😜" 😂😂😂
© 2020-2023 Hart und Trocken | Impressum | Datenschutz | Coverband Stuttgart
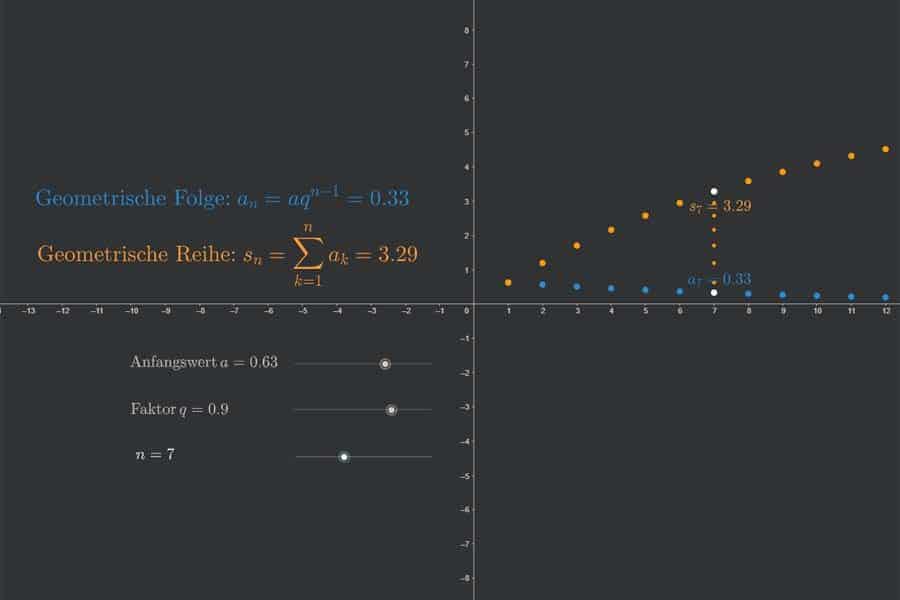
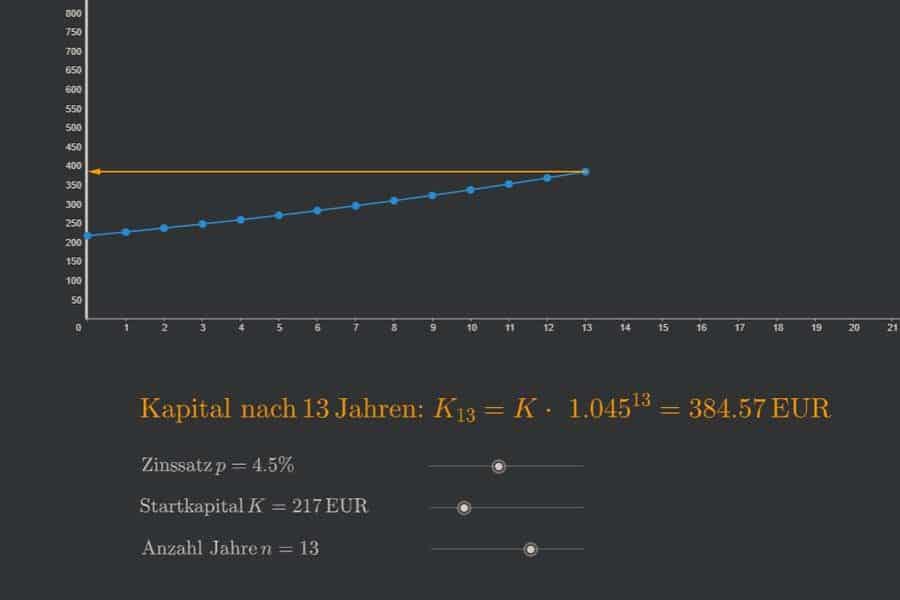
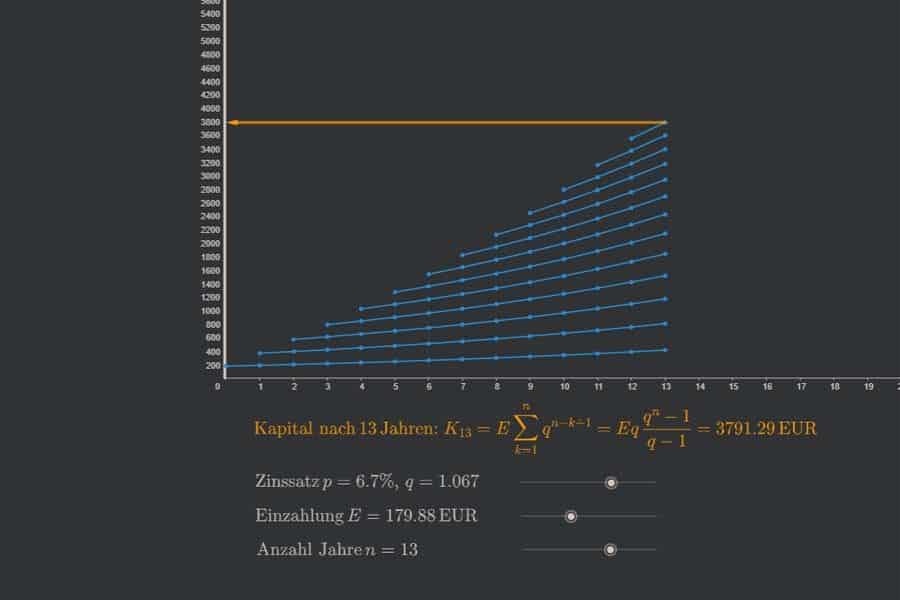
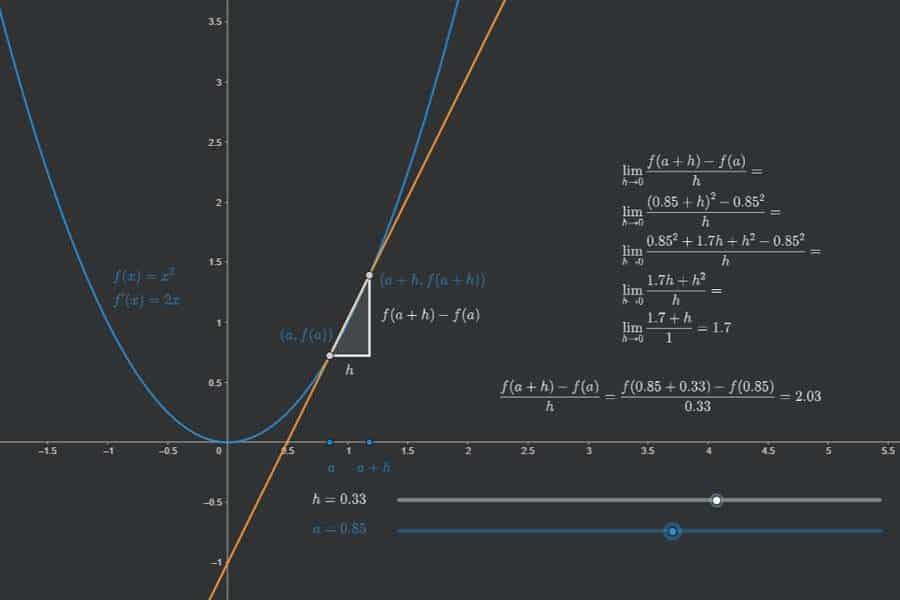
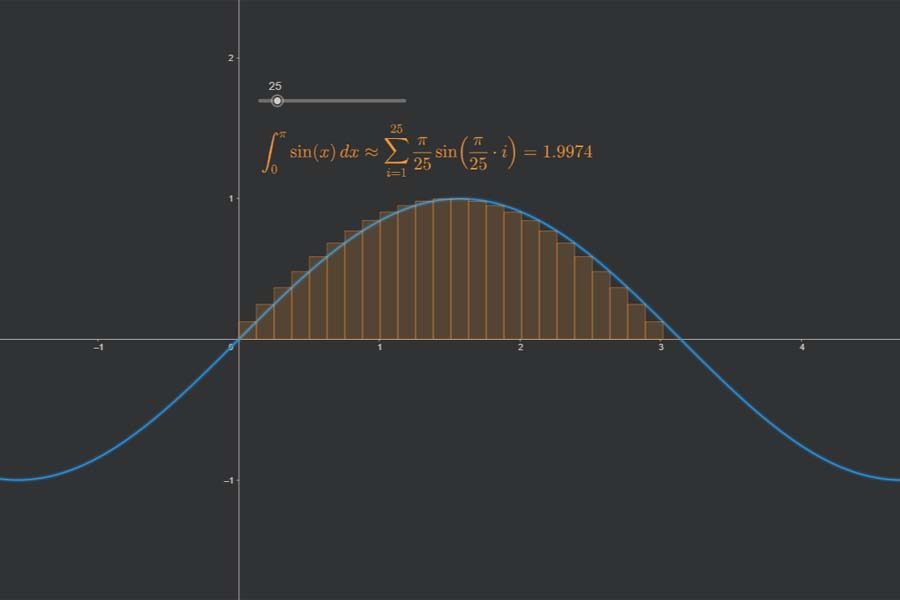
Interaktiv: Arithmetische Folge und Reihe