Wie hätten Sie Ihre komplexe Zahl gern? Kartesisch, polar oder nach Euler-Art? Wir haben alles.
Die Wurzel ist die Wurzel allen Übels. Wenn man so will. Denn wäre das Wurzelziehen bei den reellen, und insbesondere bei den unbequemen negativen Zahlen kein Problem, hätte man die komplexen Zahlen erst gar nicht ersinnen müssen. So aber mussten sie eingeführt werden, und jetzt müssen sie auf den mathematischen Zahnarztstuhl. Wurzelbehandlung. Das Schöne ist: Jede von ihnen hat genau n verschiedene n-te Wurzeln, und die sind auch noch hübsch angeordnet – wie auf einer Geburtstagstorte. Happy Birthday.


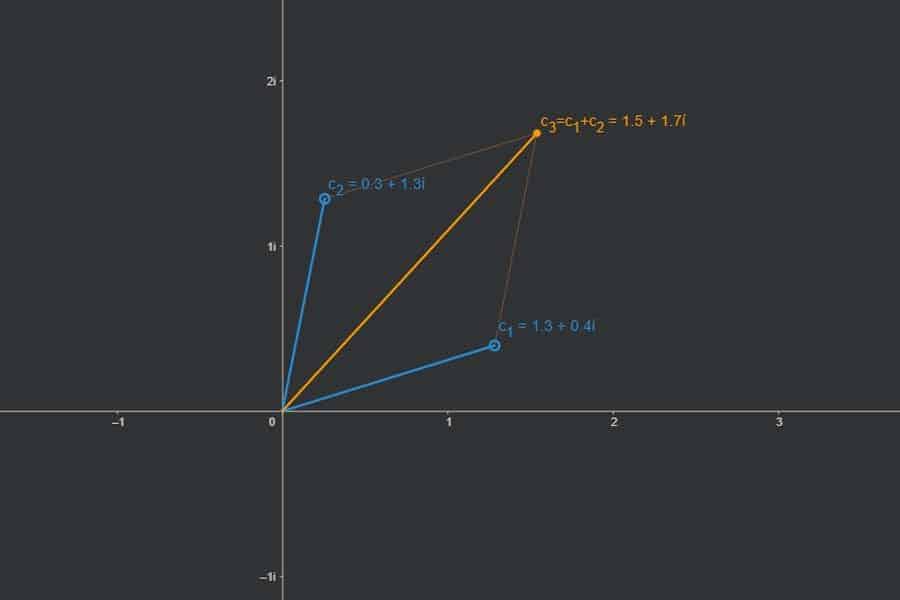
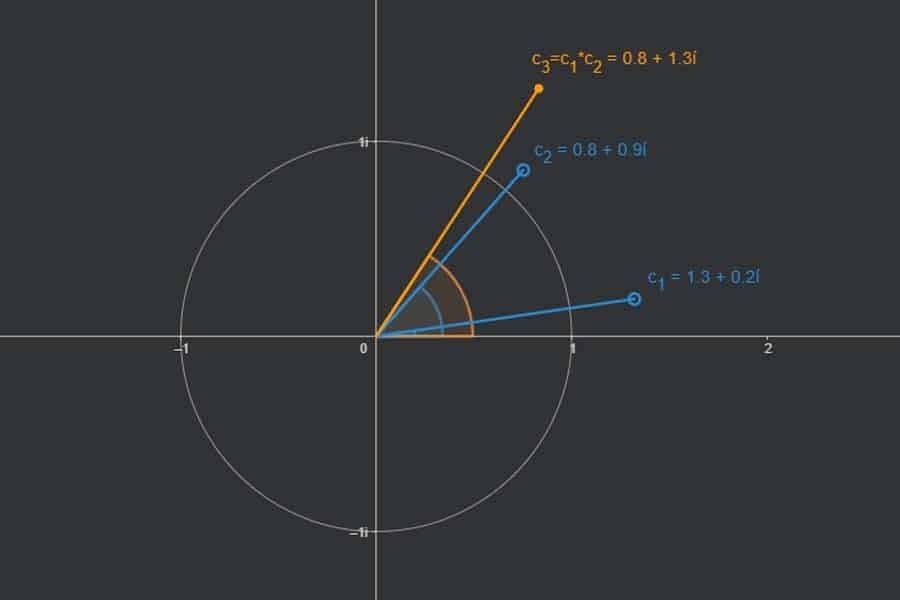
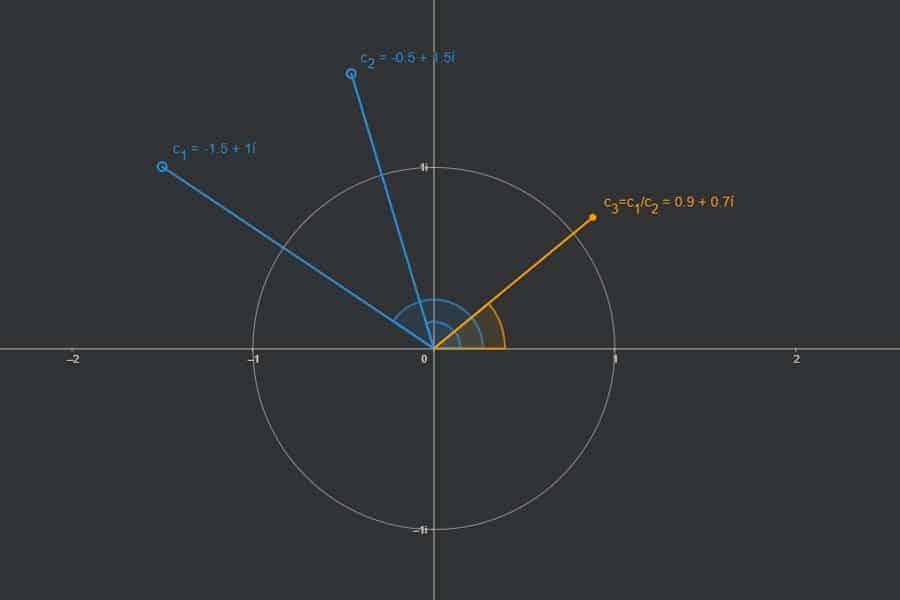













Interaktiv: Darstellungen komplexer Zahlen